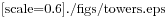Appendix B Analisi degli Algoritmi
Questa Appendice è un estratto adattato da Think Complexity, di Allen B. Downey, pure pubblicato da O’Reilly Media (2012). Quando avete finito questo libro, vi invito a prenderlo in considerazione.
L’analisi degli algoritmi è una branca dell’informatica che studia le prestazioni degli algoritmi, in particolare il tempo di esecuzione e i requisiti di memoria. Vedere anche http://en.wikipedia.org/wiki/Analysis_of_algorithms.
L’obiettivo pratico dell’analisi degli algoritmi è predire le prestazioni di algoritmi diversi in modo da orientare le scelte di progettazione.
Durante la campagna elettorale per le Presidenziali degli Stati Uniti del 2008, al candidato Barack Obama fu chiesto di fare un’analisi estemporanea in occasione della sua visita a Google. Il direttore esecutivo Eric Schmidt gli chiese scherzosamente “il modo più efficiente di ordinare un milione di interi a 32-bit”. Obama era stato presumibilmente messo sull’avviso, poiché replicò subito: “Credo che un ordinamento a bolle sarebbe il modo sbagliato di procedere”. Vedere http://www.youtube.com/watch?v=k4RRi_ntQc8.
È vero: l’ordinamento a bolle, o “bubble sort”, è concettualmente semplice ma è lento per grandi insiemi di dati. La risposta che Schmidt probabilmente si aspettava era “radix sort” (http://it.wikipedia.org/wiki/Radix_sort)1.
Scopo dell’analisi degli algoritmi è fare dei confronti significativi tra algoritmi, ma occorre tener conto di alcuni problemi:
- L’efficienza relativa degli algoritmi può dipendere dalle caratteristiche dell’hardware, per cui un algoritmo può essere più veloce sulla Macchina A, un altro sulla Macchina B. La soluzione in genere è specificare un modello di macchina e quindi analizzare il numero di passi, o operazioni, che un algoritmo richiede su quel dato modello.
- L’efficienza relativa può dipendere da alcuni dettagli dell’insieme di dati, Per esempio, alcuni algoritmi di ordinamento sono più veloci se i dati sono già parzialmente ordinati; altri in casi simili sono più lenti. Un modo di affrontare il problema è di analizzare lo scenario del caso peggiore. Talvolta è utile anche analizzare le prestazioni del caso medio, ma questo comporta più difficoltà e può non essere facile stabilire quale insieme di dati mediare.
- L’efficienza relativa dipende anche dalle dimensioni del problema. Un algoritmo di ordinamento che è veloce per liste corte può diventare lento su liste lunghe. La soluzione più comune è di esprimere il tempo di esecuzione (o il numero di operazioni) in funzione delle dimensioni del problema, e raggruppare le funzioni in categorie a seconda di quanto velocemente crescono al crescere delle dimensioni del problema.
Il lato buono di questo tipo di confronto è che conduce a una semplice classificazione degli algoritmi. Ad esempio, se sappiamo che il tempo di esecuzione dell’algoritmo A tende ad essere proporzionale alle dimensioni dell’input, n, e l’algoritmo B tende ad essere proporzionale a n2, allora possiamo attenderci che A sia più veloce di B, almeno per grandi valori di n.
Questo tipo di analisi ha alcune avvertenze, ma ci torneremo più avanti.
B.1 Ordine di complessità
Supponiamo che abbiate analizzato due algoritmi esprimendo i loro tempi di esecuzione in funzione delle dimensioni dell’input: l’Algoritmo A impiega 100n+1 operazioni per risolvere un problema di dimensione n; l’Algoritmo B impiega n2 + n + 1 operazioni.
La tabella seguente mostra il tempo di esecuzione di questi algoritmi per diverse dimensioni del problema:
| Dimensione | Tempo | Tempo |
| dell’input | Algoritmo A | Algoritmo B |
| 10 | 1 001 | 111 |
| 100 | 10 001 | 10 101 |
| 1 000 | 100 001 | 1 001 001 |
| 10 000 | 1 000 001 | > 1010 |
Per n=10, l’Algoritmo A si comporta piuttosto male: impiega quasi 10 volte il tempo dell’Algoritmo B. Ma per n=100 sono circa equivalenti, e per grandi valori A è molto migliore.
Il motivo fondamentale è che, per grandi valori di n, ogni funzione che contiene un termine n2 crescerà più rapidamente di una che ha come termine dominante n. L’operazione dominante è quella relativa al termine con il più alto esponente.
Per l’algoritmo A, l’operazione dominante ha un grande coefficiente, 100, ed è per questo che B è migliore di A per piccoli valori di n. Ma indipendentemente dal coefficiente, esisterà un valore di n a partire dal quale a n2 > b n, qualunque siano i valori di a e b.
Stesso discorso vale per i termini secondari. Anche se il tempo di esecuzione dell’Algoritmo A fosse n+1000000, sarebbe sempre migliore di B per valori sufficientemente grandi di n.
In genere, possiamo aspettarci che un algoritmo con piccola operazione dominante sia migliore per problemi di dimensione maggiore, ma per quelli di minori dimensioni può esistere un punto di intersezione dove un altro algoritmo diventa migliore. Questo punto dipende dai dettagli dell’algoritmo, dai dati di input e dall’hardware, quindi di solito è trascurato per gli scopi dell’analisi degli algoritmi. Ma non significa che dobbiate scordarvene.
Se due algoritmi hanno l’operazione dominante dello stesso ordine, è difficile stabilire quale sia migliore; ancora, la risposta dipende dai dettagli. Per l’analisi degli algoritmi, le funzioni dello stesso ordine sono considerate equivalenti, anche se hanno coefficienti diversi.
Un ordine di complessità è dato da un insieme di funzioni il cui comportamento di crescita è considerato equivalente. Per esempio, 2n, 100n e n+1 appartengono allo stesso ordine di complessità, che si scrive O(n) nella notazione O-grande e viene chiamato lineare perché tutte le funzioni dell’insieme crescono in maniera lineare al crescere di n.
Tutte le funzioni con operazione dominante n2 appartengono a O(n2) e sono dette quadratiche.
La tabella seguente mostra alcuni degli ordini di complessità più comuni nell’analisi degli algoritmi, in ordine crescente di inefficienza.
| Ordine di | Nome |
| complessità | |
| O(1) | costante |
| O(logb n) | logaritmico (per qualunque b) |
| O(n) | lineare |
| O(n logb n) | linearitmico |
| O(n2) | quadratico |
| O(n3) | cubico |
| O(cn) | esponenziale (per qualunque c) |
Per i termini logaritmici, la base del logaritmo non ha importanza; cambiare base equivale a moltiplicare per una costante, il che non modifica l’ordine di complessità. Allo stesso modo, tutte le funzioni esponenziali appartengono allo stesso ordine indipendentemente dall’esponente. Dato che le funzioni esponenziali crescono molto velocemente, gli algoritmi esponenziali sono utili solo per problemi di piccole dimensioni.
Leggete la pagina di Wikipedia sulla notazione O-grande: http://it.wikipedia.org/wiki/O-grande e rispondete alle seguenti domande:
- Qual è l’ordine di complessità di n3 + n2? E di 1000000 n3 + n2? E di n3 + 1000000 n2?
- Qual è l’ordine di complessità (n2 + n) · (n + 1)? Prima di iniziare a moltiplicare, ricordate che vi interessa solo l’operazione dominante.
- Se f appartiene a O(g), per una non specificata funzione g, cosa possiamo dire di af+b?
- Se f1 e f2 appartengono a O(g), cosa possiamo dire di f1 + f2?
- Se f1 appartiene a O(g) e f2 appartiene a O(h), cosa possiamo dire di f1 + f2?
- Se f1 appartiene a O(g) e f2 appartiene a O(h), cosa possiamo dire di f1 · f2?
I programmatori attenti alle prestazioni sono spesso critici su questo tipo di analisi. Ne hanno un motivo: a volte i coefficienti e i termini secondari fanno davvero differenza. E a volte i dettagli dell’hardware, del linguaggio di programmazione, e delle caratteristiche dell’input fanno una grande differenza. E per i piccoli problemi, l’analisi asintotica è irrilevante.
Ma tenute presenti queste avvertenze, l’analisi degli algoritmi è uno strumento utile. Almeno per i grandi problemi, l’algoritmo “migliore” è effettivamente migliore, e a volte molto migliore. La differenza tra due algoritmi dello stesso ordine di solito è un fattore costante, ma la differenza tra un buon algoritmo e uno cattivo è illimitata!
B.2 Analisi delle operazioni fondamentali di Python
In Python, molte operazioni aritmetiche sono a tempo costante: di solito la moltiplicazione impiega più tempo di addizione e sottrazione, e la divisione impiega ancora di più, ma i tempi di esecuzione sono indipendenti dalla grandezza degli operandi. Fanno eccezione gli interi molto grandi: in tal caso il tempo di elaborazione cresce al crescere del numero delle cifre.
Le operazioni di indicizzazione—lettura e scrittura di elementi di una sequenza o dizionario—sono anch’esse a tempo costante, indipendentemente dalle dimensioni della struttura di dati.
Un ciclo for che attraversa una sequenza o un dizionario è di solito lineare, a patto che tutte le operazioni nel corpo del ciclo siano a tempo costante. Per esempio, la sommatoria degli elementi di una lista è lineare:
totale = 0
for x in t:
totale += x
La funzione predefinita sum è pure lineare, visto che fa la stessa cosa, ma tende ad essere più rapida perché è un’implementazione più efficiente: nel linguaggio dell’analisi degli algoritmi, ha un coefficiente dell’operazione dominante più piccolo.
Come regola di massima, se il corpo di un ciclo appartiene a O(na) allora il ciclo nel suo complesso appartiene a O(na+1). Fa eccezione il caso in cui il ciclo esce dopo un numero di iterazioni costante. Se un ciclo viene eseguito per k volte indipendentemente da n, allora il ciclo appartiene a O(na), anche per grandi valori di k.
Moltiplicare per k non cambia l’ordine di complessità, ma nemmeno dividere. Pertanto se il corpo del ciclo appartiene O(na) e viene eseguito n/k volte, il ciclo appartiene a O(na+1), anche per grandi valori di k.
La maggioranza delle operazioni su stringhe e tuple sono lineari, eccetto l’indicizzazione e len, che sono a tempo costante. Le funzioni predefinite min e max sono lineari. Il tempo di esecuzione dello slicing è proporzionale alla lunghezza del risultato, ma indipendente dalle dimensioni del dato di partenza.
Il concatenamento di stringhe è lineare. Il tempo di esecuzione dipende dalla somma delle lunghezze degli operandi.
Tutti i metodi delle stringhe sono lineari, ma se le lunghezze delle stringhe sono limitate da una costante—ad esempio operazioni su singoli caratteri—sono considerati a tempo costante. Il metodo delle stringhe join è lineare, e il tempo di esecuzione dipende dalla lunghezza totale delle stringhe.
La maggior parte dei metodi delle liste sono lineari, con alcune eccezioni:
- L’aggiunta di un elemento alla fine di una lista è mediamente a tempo costante; quando si supera lo spazio disponibile, occasionalmente la lista viene copiata in uno spazio più ampio, ma il tempo totale per n operazioni è O(n), quindi il tempo medio di ciascuna operazione è O(1).
- La rimozione di un elemento dalla fine della lista è a tempo costante.
- L’ordinamento appartiene a O(n logn).
La maggior parte delle operazioni e dei metodi dei dizionari sono lineari, con alcune eccezioni:
- Il tempo di esecuzione di update è proporzionale alle dimensioni del dizionario passato come parametro, non del dizionario che viene aggiornato.
- keys, values e items sono a tempo costante perché restituiscono iteratori. Ma se attraversate con un ciclo un iteratore, il ciclo sarà lineare.
Le prestazioni dei dizionari sono uno dei piccoli miracoli dell’informatica. Vedremo come funzionano nel Paragrafo B.4.
Leggete la pagina di Wikipedia sugli algoritmi di ordinamento: http://it.wikipedia.org/wiki/Algoritmo_di_ordinamento e rispondete alle seguenti domande:
- Che cos’è un ordinamento per confronto (“comparison sort”)? Qual è l’ordine di complessità minimo, nel peggiore dei casi, per un ordinamento per confronto? Qual è l’ordine di complessità minimo, nel peggiore dei casi, per qualsiasi algoritmo di ordinamento?
- Qual è l’ordine di complessità dell’ordinamento a bolle (o bubblesort), e perché Barack Obama pensa che sia “il modo sbagliato di procedere”?
- Qual è l’ordine di complessità del radix sort? Quali precondizioni devono essere soddisfatte per poterlo usare?
- Che cos’è un ordinamento stabile (“stable sort”) e perché è interessante in pratica?
- Qual è il peggior algoritmo di ordinamento (tra quelli che hanno un nome)?
- Quale algoritmo di ordinamento usa la libreria C? Quale usa Python? Questi algoritmi sono stabili? Eventualmente fate alcune ricerche sul web per trovare le risposte.
- Molti degli ordinamenti che non operano per confronto sono lineari, allora perché Python usa un ordinamento per confronto di tipo O(n logn) ?
B.3 Analisi degli algoritmi di ricerca
Una ricerca è un algoritmo che, data una raccolta e un elemento, determina se l’elemento appartiene alla raccolta, restituendo di solito il suo indice.
Il più semplice algoritmo di ricerca è una “ricerca lineare”, che attraversa gli elementi della raccolta nel loro ordine, fermandosi se trova quello che cerca. Nel caso peggiore, dovrà attraversare tutta la raccolta, quindi il tempo di esecuzione è lineare.
L’operatore in delle sequenze usa una ricerca lineare, come pure i metodi delle stringhe find e count.
Se gli elementi della sequenza sono ordinati, potete usare una ricerca binaria, che appartiene a O(logn). È simile all’algoritmo che usate per cercare una voce quando consultate un vocabolario. Invece di partire dall’inizio e controllare ogni voce nell’ordine, cominciate con un elemento nel mezzo e controllate se quello che cercate viene prima o dopo. Se viene prima, cercate nella prima metà della sequenza, altrimenti nella seconda metà. In ogni caso, dimezzate il numero di elementi rimanenti.
Se una sequenza ha 1.000.000 di elementi, ci vorranno al massimo una ventina di passaggi per trovare la parola o concludere che non esiste. Quindi è circa 50.000 volte più veloce di una ricerca lineare.
La ricerca binaria può essere molto più veloce di quella lineare, ma richiede che la sequenza sia ordinata, il che può comportare del lavoro supplementare.
Esiste un’altra struttura di dati, chiamata tabella hash, che è ancora più veloce—è in grado di effettuare una ricerca a tempo costante—e non richiede che gli elementi siano ordinati. I dizionari di Python sono implementati usando tabelle hash, e questo è il motivo per cui la maggior parte delle operazioni sui dizionari, incluso l’operatore in, sono a tempo costante.
B.4 Tabelle hash
Per spiegare come funzionano le tabelle hash e perché le loro prestazioni sono così buone, inizierò con un’implementazione semplice di una mappatura e la migliorerò gradualmente fino a farla diventare una tabella hash.
Per illustrare questa implementazione userò Python, ma in pratica non scriverete mai codice del genere in Python: userete semplicemente un dizionario! Pertanto, per il resto di questo capitolo immaginate che i dizionari non esistano, e di voler implementare una struttura di dati che fa corrispondere delle chiavi a dei valori. Le operazioni che bisogna implementare sono:
- add(k, v):
- Aggiunge un nuovo elemento che fa corrispondere la chiave k al valore v. Con un dizionario Python, d, questa operazione si scrive d[k] = v.
- get(k):
- Cerca e restituisce il valore corrispondente alla chiave k. Con un dizionario Python, d, questa operazione si scrive d[k] oppure d.get(k).
Per ora, supponiamo che ogni chiave compaia solo una volta. L’implementazione più semplice di questa interfaccia usa una lista di tuple, dove ogni tupla è una coppia chiave-valore.
class MappaLineare:
def __init__(self):
self.items = []
def add(self, k, v):
self.items.append((k, v))
def get(self, k):
for chiave, valore in self.items:
if chiave == k:
return valore
raise KeyError
add accoda una tupla chiave-valore alla lista di elementi, operazione che è a tempo costante.
get usa un ciclo for per ricercare nella lista: se trova la chiave target restituisce il corrispondente valore, altrimenti solleva un KeyError. Quindi get è lineare.
Un’alternativa è mantenere la lista ordinata per chiavi. Allora, get potrebbe usare una ricerca binaria, che appartiene a O(logn). Ma l’inserimento di un nuovo elemento in mezzo a una lista è lineare, quindi questa potrebbe non essere l’opzione migliore. Esistono altre strutture di dati in grado di implementare add e get in tempo logaritmico, ma non va ancora così bene come il tempo costante, quindi andiamo avanti.
Un modo di migliorare MappaLineare è di spezzare la lista di coppie chiave-valore in liste più piccole. Ecco un’implementazione chiamata MappaMigliore, che è una lista di 100 MappeLineari. Vedremo in un istante che l’ordine di complessità di get è sempre lineare, ma MappaMigliore è un passo in direzione delle tabelle hash:
class MappaMigliore:
def __init__(self, n=100):
self.maps = []
for i in range(n):
self.maps.append(MappaLineare())
def trova_mappa(self, k):
indice = hash(k) % len(self.maps)
return self.maps[indice]
def add(self, k, v):
m = self.trova_mappa(k)
m.add(k, v)
def get(self, k):
m = self.trova_mappa(k)
return m.get(k)
__init__ crea una lista di n MappeLineari.
trova_mappa è usata da
add e get per capire in quale mappatura inserire il nuovo elemento o in quale mappatura ricercare.
trova_mappa usa la funzione predefinita hash, che accetta pressoché qualunque oggetto Python e restituisce un intero. Un limite di questa implementazione è che funziona solo con chiavi a cui è applicabile un hash, e i tipi mutabili come liste e dizionari non lo sono.
Gli oggetti hash-abili che vengono considerati equivalenti restituiscono lo stesso valore hash, ma l’inverso non è necessariamente vero: due oggetti con valori diversi possono restituire lo stesso valore hash.
trova_mappa usa l’operatore modulo per inglobare i valori hash nell’intervallo da 0 a len(self.maps), in modo che il risultato sia un indice valido per la lista. Naturalmente, ciò significa che molti valori hash diversi saranno inglobati nello stesso indice. Ma se la funzione hash distribuisce le cose abbastanza uniformemente (che è quello per cui le funzioni hash sono progettate), possiamo attenderci n/100 elementi per MappaLineare.
Siccome il tempo di esecuzione di MappaLineare.get è proporzionale al numero di elementi, possiamo attenderci che MappaMigliore sia circa 100 volte più veloce di MappaLineare. L’ordine di complessità è sempre lineare, ma il coefficiente dell’operazione dominante è più piccolo. Risultato discreto, ma non ancora come una tabella hash.
Ed ecco (finalmente) il punto cruciale che rende veloci le tabelle hash: se riuscite a mantenere limitata la lunghezza massima delle MappeLineari, MappaLineare.get diventa a tempo costante. Quello che bisogna fare è tenere conto del numero di elementi, e quando questo numero per MappaLineare eccede una soglia, ridimensionare la tabella hash aggiungendo altre MappeLineari.
Ecco un’implementazione di una tabella hash:
class MappaHash:
def __init__(self):
self.maps = MappaMigliore(2)
self.num = 0
def get(self, k):
return self.maps.get(k)
def add(self, k, v):
if self.num == len(self.maps.maps):
self.resize()
self.maps.add(k, v)
self.num += 1
def ridimensiona(self):
new_maps = MappaMigliore(self.num * 2)
for m in self.maps.maps:
for k, v in m.items:
new_maps.add(k, v)
self.maps = new_maps
Ogni MappaHash contiene una MappaMigliore; __init__ comincia con sole 2 MappeLineari e inizializza num, che tiene il conto del numero di elementi.
get rinvia semplicemente a MappaMigliore. Il lavoro vero si svolge in add, che controlla il numero di elementi e le dimensioni di MappaMigliore: se sono uguali, il numero medio di elementi per MappaLineare è 1, quindi chiama ridimensiona.
ridimensiona crea una nuova MappaMigliore, di capienza doppia della precedente, e ricalcola l’hash degli elementi dalla vecchia mappatura alla nuova.
Il ricalcolo è necessario perché cambiare il numero di MappeLineari cambia il denominatore dell’operatore modulo in trova_mappa. Ciò significa che alcuni oggetti che erano hashati nella stessa MappaLineare saranno separati (che era quello che volevamo, no?).
Il ricalcolo dell’hash è lineare, quindi ridimensiona è lineare, il che può sembrare negativo dato che mi ripromettevo che add diventasse a tempo costante. Ma ricordate che non dobbiamo ridimensionare ogni volta, quindi add è di norma costante e solo qualche volta lineare. Il lavoro complessivo per eseguire add n volte è proporzionale a n, quindi il tempo medio di ogni add è costante!
Per capire come funziona, supponiamo di iniziare con una tabella hash vuota e aggiungere una sequenza di elementi. Iniziamo con 2 MappeLineari, quindi le prime 2 aggiunte saranno veloci (nessun ridimensionamento richiesto). Diciamo che richiedono una unità lavoro ciascuna. L’aggiunta successiva richiede il ridimensionamento, e dobbiamo ricalcolare l’hash dei primi due elementi (diciamo 2 unità lavoro in più), quindi aggiungere il terzo elemento (1 altra unità). Aggiungere l’elemento successivo costa 1 unità, e in totale fanno 6 unità lavoro per 4 elementi.
Il successivo add costa 5 unità, ma i tre successivi solo 1 unità ciascuno, in totale 14 unità per 8 aggiunte.
L’aggiunta successiva costa 9 unità, ma poi possiamo aggiungerne altre 7 prima del ridimensionamento successivo, per un totale di 30 unità lavoro per le prime 16 aggiunte.
Dopo 32 aggiunte, il costo totale è 62 unità, e spero stiate cominciando ad avere chiaro lo schema. Dopo n aggiunte, con n potenza di 2, il costo totale è 2n−2 unità, per cui il lavoro medio per aggiunta è poco meno di 2 unità. Con n potenza di 2 si ha il caso migliore; per altri valori di n il lavoro medio è leggermente più alto, ma non in modo importante. La cosa importante è che sia O(1).
La Figura B.1 illustra graficamente il funzionamento. Ogni quadrato è una unità di lavoro. Le colonne mostrano il lavoro totale per ogni aggiunta nell’ordine da sinistra verso destra: le prime due aggiunte costano 1 unità, la terza 3, ecc.
Il lavoro supplementare di ricalcolo appare come una sequenza di torri sempre più alte e con spazi sempre più ampi tra due torri successive. Ora, se abbattete le torri, spalmando il costo del ridimensionamento su tutte le aggiunte, potete vedere graficamente che il costo del lavoro totale dopo n aggiunte è 2n − 2.
Una caratteristica importante di questo algoritmo è che quando ridimensioniamo la tabella hash, cresce geometricamente, cioè moltiplichiamo la dimensione per una costante. Se incrementaste le dimensioni aritmeticamente, aggiungendo ogni volta un numero fisso, il tempo medio per aggiunta sarebbe lineare.
Potete scaricare la mia implementazione di MappaHash da http://thinkpython2/code/Map.py, ma ricordate che non c’è alcuna buona ragione per usarla. Piuttosto, se dovete fare una mappatura, usate un dizionario di Python.
B.5 Glossario
- analisi degli algoritmi:
- Un modo di confrontare gli algoritmi in termini di tempo di esecuzione e/o requisiti di memoria.
- modello di macchina:
- Rappresentazione semplificata di un computer usato per analizzare il comportamento degli algoritmi.
- caso peggiore:
- L’input che, con riferimento ad un algoritmo, lo rende più lento nell’esecuzione o richiede più spazio di memoria.
- operazione dominante:
- In un polinomio, il termine con il più alto esponente.
- punto di intersezione:
- La dimensione del problema per cui due diversi algoritmi richiedono lo stesso tempo di esecuzione o lo stesso spazio di memoria.
- ordine di complessità:
- Insieme di funzioni che, per gli scopi dell’analisi degli algoritmi, crescono in maniera equivalente. Per esempio, tutte le funzioni con incremento lineare appartengono allo stesso ordine di complessità.
- Notazione O-grande:
- Notazione per rappresentare l’ordine di complessità; ad esempio, O(n) rappresenta l’insieme delle funzioni con incremento lineare.
- lineare:
- Un algoritmo il cui tempo di esecuzione è proporzionale alle dimensioni del problema, almeno per i problemi di grandi dimensioni.
- quadratico:
- Un algoritmo il cui tempo di esecuzione è proporzionale a n2, dove n è una misura delle dimensioni del problema.
- ricerca:
- Il problema di rintracciare un elemento in un insieme (come una lista o un dizionario) oppure stabilire che non è presente.
- tabella hash:
- Struttura di dati che rappresenta una raccolta di coppie chiave-valore e ne esegue la ricerca a tempo costante.
- 1
- Ma se vi capita una domanda come questa in un’intervista, ritengo che una risposta migliore sarebbe: “Il modo più rapido di ordinare un milione di interi è usare una qualsiasi funzione di ordinamento di cui dispone il linguaggio di programmazione che uso. Il suo rendimento sarà abbastanza buono per la maggior parte delle applicazioni, ma se proprio capitasse che la mia fosse troppo lenta, userei un profiler per controllare dove viene impiegato il tempo. Se risultasse che un algoritmo di ordinamento più rapido avrebbe un impatto significativo sulle prestazioni, cercherei una buona implementazione del radix sort”.
Contribute
If you would like to make a contribution to support my books, you can use the button below. Thank you!
Are you using one of our books in a class?
We'd like to know about it. Please consider filling out this short survey.