Numpy 1: introduzione¶

Riferimenti: SoftPython - numpy 1

  • visualizza al meglio in
  • versione stampabile: clicca qua
  • per navigare nelle slide: premere Esc


Summer School Data Science 2023 - Modulo 1 informatica: Moodle

Docente: David Leoni david.leoni@unitn.it

Esercitatore: Luca Bosotti luca.bosotti@studenti.unitn.it

Matrici - IL RITORNO¶

matrice

...stavolta efficienti!¶

Matrici¶

Ci sono sostanzialmente due modi in Python di rappresentare matrici:

Liste di liste (già viste):

  1. native in Python
  2. non efficienti
  3. le liste sono pervasive in Python, probabilmente incontrerai matrici espresse come liste di liste in ogni caso
  4. forniscono un'idea di come costruire una struttura dati annidata
  5. possono servire per comprendere concetti importanti come puntatori alla memoria e copie

Numpy: SoftPython - numpy

  1. non nativamente disponibile in Python
  2. efficienti
  3. alla base di parecchie librerie di calcolo scientifico (scipy, pandas)
  4. la sintassi per accedere agli elementi lievemente diversa da quella da liste di liste
  5. in rari casi potrebbe portare problemi di installazione e/o conflitti

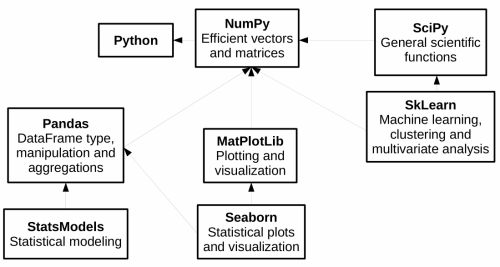
Dov'è numpy?¶

np.array¶

In [2]:
import numpy as np   #  rinominiamo in `np`

  • numpy di solito crea in un colpo solo tutta la matrice

  • regione contigua di memoria

In [3]:
mat = np.zeros(  (2,3)  )   # UN SOLO PARAMETRO tupla: 2 righe, 3 colonne
In [4]:
mat
Out[4]:
array([[0., 0., 0.],
       [0., 0., 0.]])

ATTENZIONE: anche se vedi delle quadre, gli oggetti di numpy non sono liste di liste!

In [5]:
type(mat)
Out[5]:
numpy.ndarray

Matrice da lista di liste¶

Se PROPRIO avete necessità, potete creare una matrice numpy da una lista di liste:

In [6]:
mat = np.array( [ [5.0,8.0,1.0],
                  [4.0,3.0,2.0]] )

DOMANDA: quand'è che potrebbe aver senso farlo?

DOMANDA: e se ho una matrice numpy, ha senso convertirla a lista di liste?

Matrice riempita di un numero k¶

In [7]:
np.full( (3,5), 7)
Out[7]:
array([[7, 7, 7, 7, 7],
       [7, 7, 7, 7, 7],
       [7, 7, 7, 7, 7]])

Dimensioni di una matrice¶

matrice

In [8]:
mat = np.array( [ [5.0,8.0,1.0],
                  [4.0,3.0,2.0] ] )

mat.shape
Out[8]:
(2, 3)

DOMANDA 1: Che cos'è?

DOMANDA 2: .shape è un attributo o un metodo?

Lettura e scrittura¶

ATTENZIONE: la notazione mat[i,j] funziona solo in numpy!

In [9]:
mat = np.array( [ [5.0,8.0,1.0],
                  [4.0,3.0,2.0]])
In [10]:
mat[0,1]
Out[10]:
8.0
In [11]:
mat[0,1] = 9
In [12]:
mat
Out[12]:
array([[5., 9., 1.],
       [4., 3., 2.]])

Scrittura - No fritti misti¶

Per efficienza Numpy usa regioni di memoria contigue e omogenee:

mat[0,0] = "c"

---------------------------------------------------------------------------
ValueError                                Traceback (most recent call last)
/tmp/ipykernel_45876/3318513095.py in <module>
----> 1 mat[0,0] = "c"

ValueError: could not convert string to float: 'c'

Slice¶

In [13]:
mat = np.array( [ [5, 8, 1],
                  [4, 3, 2],
                  [6, 7, 9],
                  [9, 3, 4],
                  [8, 2, 7]])

Esempio:

righe dalla 0 inclusa alla 4 esclusa

colonne dalla 1 inclusa alla 3 esclusa

In [14]:
mat[0:4, 1:3]
Out[14]:
array([[8, 1],
       [3, 2],
       [7, 9],
       [3, 4]])

Slice - esempi lettura¶

In [15]:
mat = np.array( [ [5, 8, 1],
                  [4, 3, 2],
                  [6, 7, 9],
                  [9, 3, 4]])
In [16]:
mat[0:4, 0:1]  # tutta la prima colonna
Out[16]:
array([[5],
       [4],
       [6],
       [9]])
In [17]:
mat[0:4, 0]  # ATTENZIONE: senza slice ritorna un vettore, non una matrice
Out[17]:
array([5, 4, 6, 9])
In [18]:
mat[0:1,:]   # tutta la prima riga
Out[18]:
array([[5, 8, 1]])

DOMANDA: questo cosa produce? Qual'è la differenza con sopra?     mat[0,:]

Slice - passo¶

In [19]:
mat = np.array( [ [5, 8, 1],
                  [4, 3, 2],
                  [6, 7, 9],
                  [9, 3, 4],
                  [8, 2, 7]])

mat[0:5:2, :]  # prende righe alternate
Out[19]:
array([[5, 8, 1],
       [6, 7, 9],
       [8, 2, 7]])

Slice - scrittura 1/2¶

In [20]:
mat = np.array( [ [5, 8, 1],
                  [4, 3, 2],
                  [6, 7, 9] ])
In [21]:
sotto_mat = mat[0:2, 1:3]
In [22]:
sotto_mat
Out[22]:
array([[8, 1],
       [3, 2]])

Slice - scrittura 2/2¶

In [23]:
sotto_mat[0,0] = 999
In [24]:
sotto_mat
Out[24]:
array([[999,   1],
       [  3,   2]])
In [25]:
mat
Out[25]:
array([[  5, 999,   1],
       [  4,   3,   2],
       [  6,   7,   9]])

ATTENZIONE: modifica slice di numpy -> modifica anche la matrice originale!

Slice: scrivere una costante¶

In [26]:
mat = np.array( [ [5, 8, 1],
                  [4, 3, 2],
                  [6, 7, 9],
                  [9, 3, 4],
                  [8, 2, 5]])

mat[0:4, 1:3]  = 7

mat
Out[26]:
array([[5, 7, 7],
       [4, 7, 7],
       [6, 7, 7],
       [9, 7, 7],
       [8, 2, 5]])

Slices: Scrivere una matrice¶

ATTENZIONE: le dimensioni della slice e della matrice a destra devono coincidere!

In [27]:
mat = np.array( [ [5, 8, 1],
                  [4, 3, 2],
                  [6, 7, 9],
                  [9, 3, 4],
                  [8, 2, 5]])

mat[0:4, 1:3]  = np.array([
                            [10,50],
                            [11,51],
                            [12,52],
                            [13,53],
                        ])

mat
Out[27]:
array([[ 5, 10, 50],
       [ 4, 11, 51],
       [ 6, 12, 52],
       [ 9, 13, 53],
       [ 8,  2,  5]])

Assegnazione e copia¶

Gli array di numpy sono mutabili:

In [28]:
va = np.array([1,2,3])
In [29]:
vb = va
In [30]:
vb[0] = 100
In [31]:
vb
Out[31]:
array([100,   2,   3])
In [32]:
va
Out[32]:
array([100,   2,   3])

Copia¶

In [33]:
ma = np.array([[1,2,3],
               [4,5,6]])
In [34]:
mc = ma.copy()
In [35]:
mc
Out[35]:
array([[1, 2, 3],
       [4, 5, 6]])
In [36]:
mc[0][0] = 100
In [37]:
mc
Out[37]:
array([[100,   2,   3],
       [  4,   5,   6]])
In [38]:
ma
Out[38]:
array([[1, 2, 3],
       [4, 5, 6]])

Calcoli¶

In [39]:
va = np.array([10,20,30])
In [40]:
vb = np.array([1,2,3])

operazioni algebriche creano un NUOVO array:

In [41]:
vc = va + vb
In [42]:
vc
Out[42]:
array([11, 22, 33])
In [43]:
va
Out[43]:
array([10, 20, 30])

Moltiplicazione per uno scalare¶

In [44]:
m = np.array([[5, 9, 7],
              [6, 8, 0]])
In [45]:
m * 3
Out[45]:
array([[15, 27, 21],
       [18, 24,  0]])
In [46]:
m + 3
Out[46]:
array([[ 8, 12, 10],
       [ 9, 11,  3]])

Moltiplicazione con *¶

ATTENZIONE: * in numpy moltiplica elemento per elemento!

Richiede quindi matrici di dimensioni identiche:

In [47]:
ma = np.array([[1,  2,  3],
               [10, 20, 30]])

mb = np.array([[1,  0,  1],
               [4,  5,  6]])

ma * mb
Out[47]:
array([[  1,   0,   3],
       [ 40, 100, 180]])

Moltiplicazione righe per colonne con @¶

  • attenzione ad avere matrici di dimensioni compatibili:
In [48]:
mc = np.array([[1,  2,  3],
               [10, 20, 30]])
md = np.array([[1, 4],
               [0, 5],
               [1, 6]])

mc @ md
Out[48]:
array([[  4,  32],
       [ 40, 320]])

Divisione per uno scalare¶

In [49]:
ma = np.array([[1,  2,  0.0],
               [10, 0.0, 30]])
ma / 4
Out[49]:
array([[0.25, 0.5 , 0.  ],
       [2.5 , 0.  , 7.5 ]])

Attenzione a divisione per 0.0

print(ma / 0.0)
print("DOPO")
In [50]:
 

[[inf inf nan]
 [inf nan inf]]
DOPO
stdin:1: RuntimeWarning: divide by zero encountered in true_divide
  • l’esecuzione del programma prosegue comunque + STAMPA warning extra
  • quei nan e inf possono causare problemi

Aggregazione¶

Esempi funzioni che iniziano con np.:

In [51]:
m = np.array([[5, 4, 6],
              [3, 7, 1]])
In [52]:
np.sum(m)
Out[52]:
26
In [53]:
np.max(m)
Out[53]:
7
In [54]:
np.min(m)
Out[54]:
1

Aggregazione su riga o colonna¶

parametro axis: aggregazione colonna o riga:

In [55]:
m = np.array([[5, 4, 6],
              [3, 7, 1]])
In [56]:
np.sum(m, axis=0)   # somma ogni colonna
Out[56]:
array([ 8, 11,  7])
In [57]:
np.sum(m, axis=1)   # somma ogni riga
Out[57]:
array([15, 11])

Filtrare¶

In [58]:
mat = np.array([[5, 2, 6],
                [1, 4, 3]])
In [59]:
mat[ mat > 2 ]
Out[59]:
array([5, 6, 4, 3])
In [60]:
mat > 2    # matrice di booleani
Out[60]:
array([[ True, False,  True],
       [False,  True,  True]])

messa dentro mat[ ] funge da filtro:

In [61]:
mat[ mat > 2 ]
Out[61]:
array([5, 6, 4, 3])

Filtrare: espressioni 'booleane'¶

In [62]:
mat = np.array([[5, 2, 6],
                [1, 4, 3]])
In [63]:
mat[  (mat > 3) & (mat < 6)  ]
Out[63]:
array([5, 4])
In [64]:
mat[  (mat < 2) | (mat > 4)  ]
Out[64]:
array([5, 6, 1])

ATTENZIONE: RICORDATI LE PARENTESI TONDE TRA LE VARIE ESPRESSIONI!

prova a ometterle, che succede?

ATTENZIONE: and E or NON FUNZIONANO!

prova a usarli, che succede?

Sequenza np.arange¶

La funzione standard range Python non permette incrementi con la virgola

  • Prova a scrive range(3.2), che succede?

Usiamo invece np.arange, specificando:

  1. limite sinistro, INCLUSO
  2. destro, ESCLUSO
  3. incremento
In [65]:
np.arange(0.0, 1.0, 0.2)
Out[65]:
array([0. , 0.2, 0.4, 0.6, 0.8])

Sequenza np.linspace¶

Alternativamente, possiamo usare np.linspace, specificando:

  1. limite sinistro, INCLUSO
  2. limite destro, questa volta INCLUSO
  3. numero di ripartizioni in cui suddividere questo spazio
In [66]:
np.linspace(0, 0.8, 5)
Out[66]:
array([0. , 0.2, 0.4, 0.6, 0.8])
In [67]:
np.linspace(0, 0.8, 10)
Out[67]:
array([0.        , 0.08888889, 0.17777778, 0.26666667, 0.35555556,
       0.44444444, 0.53333333, 0.62222222, 0.71111111, 0.8       ])

NaN e infinità¶

I numeri float possono essere:

  • numeri
  • 'non numeri'
  • ..e anche infinità

A volte durante i calcoli accadono condizioni estreme, esempio:

In [68]:
10e99999999999999999999999
Out[68]:
inf
In [69]:
10e99999999999999999999999 / 10e99999999999999999999999
Out[69]:
nan

Numpy adotta lo standard IEEE 754 per l’Aritmetica in virgola mobile binaria

  • implementato in tutti i processori ( CPU )
  • vale per tutti i linguaggi di programmazione

NaN¶

NaN: Not a Number

In [70]:
import math

math.nan
Out[70]:
nan
In [71]:
type(math.nan)
Out[71]:
float
math.nan == math.nan    # che fa?

False

NaN *NON* E’ UGUALE A SE’ STESSO !!!

Rilevare i NaN¶

Per vedere se numero è un NaN, non puoi scrivere così:

In [72]:
import math

numero = math.nan
if numero == math.nan:  # SBAGLIATO
    print("Sono un NaN ")
else:
    print("numero è qualcos'altro ??")

numero è qualcos'altro ??

Invece, usa la funzione math.isnan:

In [73]:
import math
numero = math.nan
if math.isnan(numero):  # CORRETTO
    print("Sono un NaN ")
else:
    print("numero è qualcos'altro ??")

Sono un NaN

Numpy e i nan¶

In [74]:
np.nan
Out[74]:
nan
In [75]:
np.inf
Out[75]:
inf

DOMANDA: Che succede se chiamiamo np.sum(malefico) ?

In [76]:
malefico = np.array([1.0,2.0,np.nan, 3.0, np.nan])
In [77]:
np.sum(malefico)
Out[77]:
nan
In [78]:
np.nansum(malefico) # Numpy spesso offre modi per ignorare i nan
Out[78]:
6.0

Esercizi¶

SoftPython - numpy 2¶

diversi esercizi di solito con due soluzioni proposte:

  • una lenta coi for
  • una veloce senza cicli

Prima provate a risolvere senza cicli, se non riuscite usate dei for o while

(ai fini dell'esame non valuto le performance, mi basta che passi i test)

Tutorial immagini (in inglese, opzionale)¶

Un modo più interessante per imparare le matrici

In [79]: