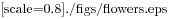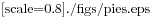Buy this book at Amazon.com

Chapter 4  Esercitazione: Progettazione dell’interfaccia

Questo capitolo vi propone un’esercitazione che dimostra una procedura per progettare delle funzioni che collaborano tra loro.

Viene illustrato il modulo grafico turtle che vi permette di creare immagini utilizzando turtle graphics. Si tratta di un modulo già compreso nella maggior parte delle installazioni di Python; tuttavia, se usate PythonAnywhere, non sarete in grado di visualizzare gli esempi basati su turtle (almeno non nel momento in cui scrivo).

Se avete già installato Python sul vostro computer, gli esempi dovrebbero funzionare. Se non lo avete ancora installato, questo è il momento buono per farlo. Ho pubblicato delle istruzioni all’indirizzo http://tinyurl.com/thinkpython2e.

Il codice degli esempi di questo capitolo è scaricabile dal sito http://thinkpython2.com/code/polygon.py

4.1  Il modulo turtle

Per controllare se il modulo turtle è installato, aprite l’interprete Python e scrivete:

>>> import turtle
>>> bob = turtle.Turtle()

Eseguendo questo codice, dovrebbe comparire una nuova finestra con un cursore a forma di freccetta che rappresenta un’ideale tartaruga. Ora chiudete pure la finestra.

Create un file di nome miopoligono.py e scriveteci il seguente codice:

import turtle
bob = turtle.Turtle()
print(bob)
turtle.mainloop()

Il modulo turtle (con la ’t’ minuscola) contiene una funzione di nome Turtle (con la ’T’ maiuscola) che crea un oggetto Turtle (una “tartaruga”); questo oggetto viene assegnato a una variabile di nome bob. Stampando bob viene visualizzato qualcosa di questo genere:

<turtle.Turtle object at 0xb7bfbf4c>

Ciò significa che bob fa riferimento ad un oggetto Turtle, come definito nel modulo turtle.

mainloop dice alla finestra di attendere che l’utente faccia qualcosa, sebbene in questo caso non ci sia molto da fare, se non chiudere la finestra.

Una volta creata una tartaruga, potete chiamare uno dei suoi metodi per spostarla in giro per la finestra. Un metodo è simile ad una funzione, ma usa una sintassi leggermente diversa. Ad esempio, per spostare la tartaruga in avanti:

bob.fd(100)

Il metodo, fd, è associato all’oggetto Turtle che abbiamo chiamato bob. Chiamare un metodo è come effettuare una richiesta: in questo caso state chiedendo a bob di muoversi in avanti [fd sta per forward, NdT]. L’argomento di fd è una distanza espressa in pixel, per cui l’effettivo spostamento dipenderà dalle caratteristiche del vostro schermo.

Altri metodi che potete chiamare su una tartaruga sono: bk per muoversi indietro (backward) e lt e rt per girare a sinistra (left) e a destra (right). Per questi ultimi due, l’argomento è un angolo espresso in gradi.

Inoltre, ogni tartaruga regge una penna, che può essere appoggiata o sollevata; se la penna è appoggiata, la tartaruga lascia un segno dove passa. I metodi pu e pd stanno per “penna su (up)” e “penna giù (down)”.

Per disegnare un angolo retto, aggiungete queste righe al programma (dopo aver creato bob e prima di chiamare mainloop):

bob.fd(100)
bob.lt(90)
bob.fd(100)

Avviando il programma, dovreste vedere bob muoversi verso destra e poi in alto, lasciandosi dietro due segmenti.

Ora provate a modificare il programma in modo da disegnare un quadrato. Non andate avanti finché non ci riuscite!

4.2  Ripetizione semplice

Probabilmente avete scritto qualcosa del genere:

bob.fd(100)
bob.lt(90)

bob.fd(100)
bob.lt(90)

bob.fd(100)
bob.lt(90)

bob.fd(100)

Si può ottenere lo stesso risultato in modo più conciso con un’istruzione for. Aggiungete questo esempio a miopoligono.py ed eseguitelo di nuovo:

for i in range(4):
    print('Ciao!')

Dovreste vedere qualcosa di simile:

Ciao!
Ciao!
Ciao!
Ciao!

Questo è l’utilizzo più semplice dell’istruzione for; ne vedremo altri più avanti. Ma questo dovrebbe bastare per permettervi di riscrivere il vostro programma di disegno di quadrati. Proseguite nella lettura solo dopo averlo fatto.

Ecco l’istruzione for che disegna un quadrato:

for i in range(4):
    bob.fd(100)
    bob.lt(90)

La sintassi di un’istruzione for è simile a quella di una funzione. Ha un’intestazione che termina con i due punti e un corpo indentato che può contenere un numero qualunque di istruzioni.

Un’istruzione for è chiamata anche ciclo, perché il flusso dell’esecuzione ne attraversa il corpo per poi ritornare indietro e ripeterlo da capo. In questo caso, il corpo viene eseguito per quattro volte.

Questa versione del disegno di quadrati è in realtà un pochino differente dalla precedente, in quanto provoca un’ultima svolta dopo aver disegnato l’ultimo lato. Ciò comporta del tempo in più, ma il codice viene semplificato, inoltre lascia la tartaruga nella stessa posizione di partenza, rivolta nella direzione iniziale.

4.3  Esercizi

Quella che segue è una serie di esercizi che utilizzano turtle. Sono pensati per essere divertenti, ma hanno anche uno scopo. Mentre ci lavorate su, provate a pensare quale sia.

I paragrafi successivi contengono le soluzioni degli esercizi, per cui non continuate la lettura finché non avete finito (o almeno provato).

1. Scrivete una funzione di nome quadrato che richieda un parametro di nome t, che è una tartaruga. La funzione deve usare la tartaruga per disegnare un quadrato.

   Scrivete una chiamata alla funzione quadrato che passi bob come argomento, ed eseguite nuovamente il programma.

2. Aggiungete a quadrato un nuovo parametro di nome lunghezza. Modificate il corpo in modo che la lunghezza dei lati sia pari a lunghezza, quindi modificate la chiamata alla funzione in modo da fornire un secondo argomento. Eseguite di nuovo il programma e provatelo con vari valori di lunghezza.
3. Fate una copia di quadrato e cambiate il nome in poligono. Aggiungete un altro parametro di nome n e modificate il corpo in modo che sia disegnato un poligono regolare di n lati. Suggerimento: gli angoli esterni di un poligono regolare di n lati misurano 360/n gradi.
4. Scrivete una funzione di nome cerchio che prenda come parametri una tartaruga, t, e un raggio, r, e che disegni un cerchio approssimato chiamando poligono con una appropriata lunghezza e numero di lati. Provate la funzione con diversi valori di r.

   Suggerimento: pensate alla circonferenza del cerchio e accertatevi che lunghezza * n = circonferenza.

5. Create una versione più generale della funzione cerchio, di nome arco, che richieda un parametro aggiuntivo angolo, il quale determina la porzione di cerchio da disegnare. angolo è espresso in gradi, quindi se angolo=360, arco deve disegnare un cerchio completo.

4.4  Incapsulamento

Il primo esercizio chiede di inserire il codice per disegnare un quadrato in una definizione di funzione, passando la tartaruga come argomento. Ecco una soluzione:

def quadrato(t):
    for i in range(4):
        t.fd(100)
        t.lt(90)

quadrato(bob)

Le istruzioni più interne, fd e lt sono doppiamente indentate per significare che si trovano all’interno del ciclo for, che a sua volta è all’interno della funzione. L’ultima riga, quadrato(bob), è a livello del margine sinistro, pertanto indica la fine sia del ciclo for che della definizione di funzione.

Dentro la funzione, t si riferisce alla stessa tartaruga a cui si riferisce bob, per cui t.lt(90) ha lo stesso effetto di bob.lt(90). Ma allora perché non chiamare bob il parametro? Il motivo è che t può essere qualunque tartaruga, non solo bob, e in questa maniera è possibile anche creare una seconda tartaruga e passarla come parametro a quadrato:

alice = turtle.Turtle()
quadrato(alice)

L’inglobare un pezzo di codice in una funzione è chiamato incapsulamento. Uno dei benefici dell’incapsulamento è che appiccica un nome al codice, il che può servire come una sorta di documentazione. Un altro vantaggio è il riuso del codice: è più conciso chiamare una funzione due volte che copiare e incollare il corpo!

4.5  Generalizzazione

Il passo successivo è aggiungere a quadrato un parametro lunghezza. Ecco una soluzione:

def quadrato(t, lunghezza):
    for i in range(4):
        t.fd(lunghezza)
        t.lt(90)

quadrato(bob, 100)

L’aggiunta di un parametro a una funzione è chiamata generalizzazione poiché rende la funzione più generale: nella versione precedente, il quadrato aveva sempre la stessa dimensione, ora può essere grande a piacere.

Anche il passo seguente è una generalizzazione. Invece di disegnare solo quadrati, poligono disegna poligoni regolari di un qualunque numero di lati. Ecco una soluzione:

def poligono(t, n, lunghezza):
    angolo = 360 / n
    for i in range(n):
        t.fd(lunghezza)
        t.lt(angolo)

poligono(bob, 7, 70)

Questo esempio disegna un ettagono regolare con lati di lunghezza 70.

Se usate Python 2, il valore di angolo può risultare impreciso, per il fatto che la divisione di due interi dà come risultato un intero (“divisione intera”, che vedremo meglio nel prossimo Capitolo). Una semplice soluzione è calcolare angolo = 360.0 / n. Dato che il numeratore ora è un numero floating-point, anche il risultato sarà un floating-point.

Quando in una chiamata di funzione avete più di qualche argomento numerico, è facile dimenticare a cosa si riferiscono o in quale ordine vanno disposti. In questi casi, è bene includere i nomi dei parametri nell’elenco degli argomenti:

poligono(bob, n=7, lunghezza=70)

Questi sono detti argomenti con nome perché includono il nome del parametro a cui vengono passati, quale “parola chiave” (da non confondere con le parole chiave riservate come while e def).

Questa sintassi rende il programma più leggibile. È anche un appunto di come funzionano argomenti e parametri: quando chiamate una funzione, gli argomenti vengono assegnati a quei dati parametri.

4.6  Progettazione dell’interfaccia

Il prossimo passaggio è scrivere cerchio, che richiede come parametro il raggio, r. Ecco una semplice soluzione che usa poligono per disegnare un poligono di 50 lati:

import math

def cerchio(t, r):
    circonferenza = 2 * math.pi * r
    n = 50
    lunghezza = circonferenza / n
    poligono(t, n, lunghezza)

La prima riga calcola la circonferenza di un cerchio di raggio r usando la nota formula 2 π r. Dato che usiamo math.pi, vi ricordo che dovete prima importare il modulo math. Per convenzione, l’istruzione import si scrive all’inizio dello script.

n è il numero di segmenti del nostro cerchio approssimato, e lunghezza è la lunghezza di ciascun segmento. Così facendo, poligono disegna un poligono di 50 lati che approssima un cerchio di raggio r.

Un limite di questa soluzione è che n è costante, il che comporta che per cerchi molto grandi i segmenti sono troppo lunghi, e per cerchi piccoli perdiamo tempo a disegnare minuscoli segmenti. Una soluzione sarebbe di generalizzare la funzione tramite un parametro n, dando all’utente (chiunque chiami la funzione cerchio) più controllo, ma rendendo così l’interfaccia meno chiara.

L’interfaccia è un riassunto di come è usata la funzione: quali sono i parametri? Che cosa fa la funzione? Qual è il valore restituito? Un’interfaccia è considerata “pulita” se permette al chiamante di fare ciò che deve, senza avere a che fare con dettagli non necessari.

In questo esempio, r appartiene all’interfaccia perché specifica il cerchio da disegnare. n è meno pertinente perché riguarda i dettagli di come il cerchio viene reso.

Piuttosto di ingombrare l’interfaccia di parametri, è meglio scegliere un valore appropriato di n che dipenda da circonferenza:

def cerchio(t, r):
    circonferenza = 2 * math.pi * r
    n = int(circonferenza / 3) + 3
    lunghezza = circonferenza / n
    poligono(t, n, lunghezza)

Ora il numero di segmenti è un numero intero vicino a circonferenza/3, e la lunghezza dei segmenti è circa 3, che è abbastanza piccolo da dare un cerchio di bell’aspetto, ma abbastanza grande da essere efficiente e appropriato per qualsiasi dimensione del cerchio.

Aggiungere 3 a n garantisce che il poligono abbia come minimo 3 lati.

4.7  Refactoring

Nello scrivere cerchio, ho potuto riusare poligono perché un poligono con molti lati è una buona approssimazione di un cerchio. Ma la funzione arco non è così collaborativa: non possiamo usare poligono o cerchio per disegnare un arco.

Un’alternativa è partire da una copia di poligono e trasformarla in arco. Il risultato può essere qualcosa del genere:

def arco(t, r, angolo):
    arco_lunghezza = 2 * math.pi * r * angolo / 360
    n = int(arco_lunghezza / 3) + 1
    passo_lunghezza = arco_lunghezza / n
    passo_angolo = angolo / n
    
    for i in range(n):
        t.fd(passo_lunghezza)
        t.lt(passo_angolo)

La seconda metà di questa funzione somiglia a poligono, ma non possiamo riusare questa funzione senza cambiarne l’interfaccia. Potremmo generalizzare poligono in modo che riceva un angolo come terzo argomento, ma allora poligono non sarebbe più un nome appropriato! Invece, creiamo una funzione più generale chiamata polilinea:

def polilinea(t, n, lunghezza, angolo):
    for i in range(n):
        t.fd(lunghezza)
        t.lt(angolo)

Ora possiamo riscrivere poligono e arco in modo che usino polilinea:

def poligono(t, n, lunghezza):
    angolo = 360.0 / n
    polilinea(t, n, lunghezza, angolo)

def arco(t, r, angolo):
    arco_lunghezza = 2 * math.pi * r * angolo / 360
    n = int(arco_lunghezza / 3) + 1
    passo_lunghezza = arco_lunghezza / n
    passo_angolo = float(angolo) / n
    polilinea(t, n, passo_lunghezza, passo_angolo)

Infine, riscriviamo cerchio in modo che usi arco:

def cerchio(t, r):
    arco(t, r, 360)

Questo procedimento di riarrangiare una programma per migliorare le interfacce e facilitare il riuso del codice, è chiamato refactoring. In questo caso, abbiamo notato che in arco e in poligono c’era del codice simile, allora abbiamo semplificato il tutto in polilinea.

Avendoci pensato prima, avremmo potuto scrivere polilinea direttamente, evitando il refactoring, ma spesso all’inizio di un lavoro non si hanno le idee abbastanza chiare per progettare al meglio tutte le interfacce. Una volta cominciato a scrivere il codice, si colgono meglio i problemi. A volte, il refactoring è segno che avete imparato qualcosa.

4.8  Tecnica di sviluppo

Una tecnica di sviluppo è una procedura di scrittura dei programmi. Quello che abbiamo usato in questa esercitazione si chiama “incapsulamento e generalizzazione”. I passi della procedura sono:

1. Iniziare scrivendo un piccolo programma senza definire funzioni.
2. Una volta ottenuto un programma funzionante, identificare una sua porzione che sia in sé coerente e autonoma, incapsularla in una funzione e dargli un nome.
3. Generalizzare la funzione aggiungendo i parametri appropriati.
4. Ripetere i passi da 1 a 3 fino ad avere un insieme di funzioni. Copiate e incollate il codice funzionante per evitare di riscriverlo (e ricorreggerlo).
5. Cercare le occasioni per migliorare il programma con il refactoring. Ad esempio, se avete del codice simile in più punti, valutate di semplificare rielaborandolo in una funzione più generale.

Questa procedura ha alcuni inconvenienti—vedremo più avanti alcune alternative—ma può essere di aiuto se in principio non sapete bene come suddividere il vostro programma in funzioni. È un approccio che vi permette di progettare man mano che andate avanti.

4.9  Stringa di documentazione

Una stringa di documentazione, o docstring, è una stringa posta all’inizio di una funzione che ne illustra l’interfaccia. Ecco un esempio:

def polilinea(t, n, lunghezza, angolo):
    """Disegna n segmenti di data lunghezza e angolo
       (in gradi) tra di loro. t e' una tartaruga.
    """    
    for i in range(n):
        t.fd(lunghezza)
        t.lt(angolo)

Per convenzione, la docstring è racchiusa tra triple virgolette, che le consentono di essere divisibile su più righe (stringa a righe multiple).

È breve, ma contiene le informazioni essenziali di cui qualcuno potrebbe aver bisogno per usare la funzione. Spiega in modo conciso cosa fa la funzione (senza entrare nei dettagli di come lo fa). Spiega che effetti ha ciascun parametro sul comportamento della funzione e di che tipo devono essere i parametri stessi (se non è ovvio).

Scrivere questo tipo di documentazione è una parte importante della progettazione dell’interfaccia. Un’interfaccia ben studiata dovrebbe essere semplice da spiegare; se fate fatica a spiegare una delle vostre funzioni, può darsi che la sua interfaccia sia migliorabile.

4.10  Debug

Un’interfaccia è simile ad un contratto tra la funzione e il suo chiamante. Il chiamante si impegna a fornire certi parametri e la funzione si impegna a svolgere un dato lavoro.

Ad esempio, a polilinea devono essere passati quattro argomenti: t deve essere una tartaruga; n deve essere un numero intero; lunghezza deve essere un numero positivo; e angolo un numero che si intende espresso in gradi.

Questi requisiti sono detti precondizioni perché si suppone siano verificati prima che la funzione sia eseguita. Per contro, le condizioni che si devono verificare al termine della funzione sono dette postcondizioni, e comprendono l’effetto che deve avere la funzione (come il disegnare segmenti) e ogni altro effetto minore (come muovere la tartaruga o fare altri cambiamenti).

Le precondizioni sono responsabilità del chiamante. Se questi viola una precondizione (documentata in modo appropriato!) e la funzione non fa correttamente ciò che deve, l’errore sta nel chiamante e non nella funzione.

Se le precondizioni sono soddisfatte e le postcondizioni no, l’errore sta nella funzione. E il fatto che le vostre pre- e postcondizioni siano chiare, è di aiuto nel debug.

4.11  Glossario

metodo:

Una funzione associata ad un oggetto che viene chiamata utlizzando la notazione a punto.

ciclo:

Una porzione di programma che può essere eseguita ripetutamente.

incapsulamento:

Il procedimento di trasformare una sequenza di istruzioni in una funzione.

generalizzazione:

Il procedimento di sostituire qualcosa di inutilmente specifico (come un numero) con qualcosa di più generale ed appropriato (come una variabile o un parametro).

argomento con nome:

Un argomento che include il nome del parametro a cui è destinato come “parola chiave”.

interfaccia:

Una descrizione di come si usa una funzione, incluso il nome, la descrizione degli argomenti e il valore di ritorno.

refactoring:

Il procedimento di modifica di un programma funzionante per miliorare le interfacce delle funzioni e altre qualità del codice.

tecnica di sviluppo:

Procedura di scrittura dei programmi.

stringa di documentazione o docstring:

Una stringa che compare all’inizio di una definizione di una funzione per documentarne l’interfaccia.

precondizione:

Un requisito che deve essere soddisfatto dal chiamante prima di eseguire una funzione.

postcondizione:

Un requisito che deve essere soddisfatto dalla funzione prima di terminare.

4.12  Esercizi

---

Figure 4.1: Fiori disegnati con turtle.

---

---

Figure 4.2: Torte disegnate con turtle.

---

Buy this book at Amazon.com

Contribute

Pay what you want:

Small $1.00 USD Medium $5.00 USD Large $10.00 USD X-Large $20.00 USD XX-Large $50.00 USD

Are you using one of our books in a class?