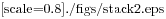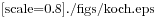Buy this book at Amazon.com

Chapter 5  Istruzioni condizionali e ricorsione

L’argomento principale di questo capitolo è l’istruzione if, che permette di eseguire codice diverso a seconda dello stato del programma. Prima di tutto, vediamo però due nuovi operatori: divisione intera e modulo.

5.1  Divisione intera e modulo

L’operatore di divisione intera, //, divide due numeri e arrotonda il risultato all’intero inferiore. Ad esempio, supponiamo che la durata di un film sia di 105 minuti, e di volerla esprimere in ore. La normale divisione restituisce un numero decimale:

>>> minuti = 105
>>> minuti / 60
1.75

Ma di solito non si esprimono le ore con un numero decimale. La divisione intera dà invece come risultato il numero di ore e tralascia la frazione di ora:

>>> minuti = 105
>>> ore = minuti // 60
>>> ore
1

Per ottenere il resto, potete sottrarre dai minuti l’equivalente delle ore:

>>> resto = minuti - ore * 60
>>> resto
45

Un’alternativa è utilizzare l’operatore modulo, %, che restituisce il resto dell’operazione di divisione tra due numeri interi.

>>> resto = minuti % 60
>>> resto
45

L’operatore modulo è più utile di quel che sembra. Per esempio, permette di controllare se un numero intero è divisibile per un altro: se x % y è zero, significa che x è divisibile per y.

Inoltre, può essere usato per estrarre la cifra più a destra di un numero: x % 10 restituisce la cifra più a destra del numero x (in base 10). Allo stesso modo, x % 100 restituisce le ultime due cifre.

Per chi usa Python 2, la divisione funziona in modo diverso. L’operatore di divisione intera non esiste, e quello di divisione, /, esegue una divisione intera se entrambi gli operandi sono interi, mentre il risultato è un decimale a virgola mobile se almeno uno degli operandi è un decimale.

5.2  Espressioni booleane

Un’espressione booleana è un’espressione che può essere o vera o falsa. Gli esempi che seguono usano l’operatore ==, confrontano due valori e restituiscono True (vero) se sono uguali, False (falso) altrimenti:

>>> 5 == 5
True
>>> 5 == 6
False

True e False sono valori speciali che sono di tipo bool; non sono delle stringhe:

>>> type(True)
<class 'bool'>
>>> type(False)
<class 'bool'>

L’operatore == è uno degli operatori di confronto; gli altri sono:

      x != y               # x è diverso da y
      x > y                # x è maggiore di y
      x < y                # x è minore di y
      x >= y               # x è maggiore o uguale a y
      x <= y               # x è minore o uguale a y

Queste operazioni vi saranno familiari, tuttavia i simboli in Python sono diversi da quelli usati comunemente in matematica. Un errore frequente è quello di usare il simbolo di uguale(=) invece del doppio uguale (==). Ricordate che = è un operatore di assegnazione, mentre == è un operatore di confronto. Inoltre in Python non esistono simboli del tipo =< o =>.

5.3  Operatori logici

Ci sono tre operatori logici: and, or, e not. Il significato di questi operatori è simile al loro significato comune (e, o, non): per esempio, l’espressione x > 0 and x < 10 è vera solo se sono vere entrambe le condizioni, cioè x è più grande di 0 e più piccolo di 10.

L’espressione n%2 == 0 or n%3 == 0 invece è vera se si verifica almeno una delle due condizioni e cioè se il numero è divisibile per 2 o per 3 (o per entrambi).

Infine, l’operatore not nega il valore di un’espressione booleana, trasformando in falsa un’espressione vera e viceversa. Così, not (x > y) è vera se x > y è falsa, cioè se x è minore o uguale a y.

In senso stretto, gli operandi degli operatori logici dovrebbero essere delle espressioni booleane, ma da questo punto di vista Python non è troppo fiscale: infatti ogni numero diverso da zero viene considerato True, e lo zero è considerato False.

>>> 42 and True
True

Questa flessibilità può essere utile, ma ci sono alcune sottigliezze che potrebbero confondere. È preferibile evitarla (a meno che non sappiate quello che state facendo).

5.4  Esecuzione condizionale

Per poter scrivere programmi utili, c’è molto spesso la necessità di valutare delle condizioni e di variare il comportamento del programma a seconda del risultato della valutazione. Le istruzioni condizionali ci offrono questa possibilità. La forma più semplice è l’istruzione if (“se” in inglese):

if x > 0:
    print("x è positivo")

L’espressione booleana dopo l’istruzione if è chiamata condizione. L’istruzione indentata che segue i due punti della riga if, viene eseguita solo se la condizione è vera. Se la condizione è falsa non viene eseguito nulla.

Come nel caso della definizione di funzione, la struttura dell’istruzione if è costituita da un’intestazione seguita da un corpo indentato. Le istruzioni come questa vengono chiamate istruzioni composte.

Non c’è limite al numero di istruzioni che possono comparire nel corpo, ma deve sempre essercene almeno una. In qualche occasione può essere utile avere un corpo vuoto, ad esempio quando il codice corrispondente non è ancora stato scritto ma si desidera ugualmente provare il programma. In questo caso si può usare l’istruzione pass, che serve solo da segnaposto temporaneo e nulla più:

if x < 0:
    pass          # scrivere cosa fare con i valori negativi!

5.5  Esecuzione alternativa

Una seconda forma di istruzione if è l’esecuzione alternativa, nella quale ci sono due azioni possibili, e il valore della condizione determina quale delle due debba essere eseguita e quale no. La sintassi è:

if x % 2 == 0:
    print("x è pari")
else:
    print("x è dispari")

Se il resto della divisione di x per 2 è zero, significa che x è un numero pari, e il programma mostra il messaggio appropriato. Se invece la condizione è falsa, viene eseguita la serie di istruzioni descritta dopo la riga else (che in inglese significa “altrimenti”). In ogni caso, una delle due alternative sarà sempre eseguita. Le due alternative sono chiamate ramificazioni, perché rappresentano dei bivi nel flusso di esecuzione del programma.

5.6  Condizioni in serie

Talvolta occorre tenere conto di più di due possibili sviluppi, pertanto possiamo aver bisogno di più di due ramificazioni. Un modo per esprimere questo tipo di calcolo sono le condizioni in serie:

if x < y:
    print("x è minore di y")
elif x > y:
    print("x è maggiore di y")
else:
    print("x e y sono uguali")

elif è l’abbreviazione di else if, che in inglese significa “altrimenti se”. Anche in questo caso, solo uno dei rami verrà eseguito, a seconda dell’esito del confronto tra x e y. Non c’è alcun limite al numero di istruzioni elif. Se esiste una clausola else, deve essere scritta per ultima, ma non è obbligatoria; il ramo corrispondente viene eseguito solo quando tutte le condizioni precedenti sono false.

if scelta == 'a':
    disegna_a()
elif scelta == 'b':
    disegna_b()
elif scelta == 'c':
    disegna_c()

Le condizioni vengono controllate nell’ordine in cui sono state scritte: se la prima è falsa viene controllata la seconda e così via. Non appena una condizione risulta vera, viene eseguito il ramo corrispondente e l’intera istruzione if si conclude. In ogni caso, anche se risultassero vere altre condizioni successive, dopo l’esecuzione della prima queste ultime verranno trascurate.

5.7  Condizioni nidificate

Si può anche inserire un’istruzione condizionale nel corpo di un’altra istruzione condizionale. Possiamo scrivere l’esempio del paragrafo precedente anche in questo modo:

if x == y:
    print("x e y sono uguali")
else:
    if x < y:
        print("x è minore di y")
    else:
        print("x è maggiore di y")

La prima condizione esterna (if x == y) contiene due rami: il primo contiene un’istruzione semplice, il secondo un’altra istruzione if che a sua volta prevede un’ulteriore ramificazione. Entrambi i rami del secondo if sono istruzioni di stampa, ma potrebbero anche contenere a loro volta ulteriori istruzioni condizionali.

Sebbene l’indentazione delle istruzioni aiuti a rendere evidente la struttura, le condizioni nidificate diventano rapidamente difficili da leggere, quindi è meglio usarle con moderazione.

Qualche volta, gli operatori logici permettono di semplificare le istruzioni condizionali nidificate:

if 0 < x:
    if x < 10:
        print("x è un numero positivo a una cifra.")

L’istruzione di stampa è eseguita solo se entrambe le condizioni si verificano. Possiamo allora usare l’operatore booleano and per combinarle:

if 0 < x and x < 10:
    print("x è un numero positivo a una cifra.")

Per una condizione di questo tipo, Python consente anche un’opzione sintattica più concisa:

if 0 < x < 10:
    print("x è un numero positivo a una cifra.")

5.8  Ricorsione

Abbiamo visto che è del tutto normale che una funzione ne chiami un’altra, ma è anche consentito ad una funzione di chiamare se stessa. L’utilità può non essere immediatamente evidente, ma questa è una delle cose più magiche che un programma possa fare. Per fare un esempio, diamo un’occhiata a questa funzione:

def contoallarovescia(n):
    if n <= 0:
        print("Via!")
    else:
        print(n)
        contoallarovescia(n-1)

Se n vale 0 o è negativo, scrive la parola “Via!”. Altrimenti scrive il numero n e poi chiama la funzione contoallarovescia (cioè se stessa) passando un argomento che vale n-1.

Cosa succede quando chiamiamo la funzione in questo modo?

>>> contoallarovescia(3)

L’esecuzione di contoallarovescia inizia da n=3, e dato che n è maggiore di 0, stampa il valore 3, poi chiama se stessa...

L’esecuzione di contoallarovescia inizia da n=2, e dato che n è maggiore di 0, stampa il valore 2, poi chiama se stessa...

L’esecuzione di contoallarovescia inizia da n=1, e dato che n è maggiore di 0, stampa il valore 1, poi chiama se stessa...

L’esecuzione di contoallarovescia inizia da n=0, e dato che n è uguale a 0, stampa la parola “Via!” e poi ritorna.

La funzione contoallarovescia che aveva dato n=1 ritorna.

La funzione contoallarovescia che aveva dato n=2 ritorna.

La funzione contoallarovescia che aveva dato n=3 ritorna.

E infine ritorniamo in __main__. Il risultato finale è questo:

3
2
1
Via!

Una funzione che chiama se stessa si dice ricorsiva e la procedura che la esegue è detta ricorsione.

Come secondo esempio, scriviamo una funzione che stampi una data stringa per n volte.

def stampa_n(s, n):
    if n <= 0:
        return
    print(s)
    stampa_n(s, n-1)

Se n <= 0 l’istruzione di ritorno return provoca l’uscita dalla funzione. Il flusso dell’esecuzione torna immediatamente al chiamante, e le righe rimanenti della funzione non vengono eseguite.

Il resto della funzione è simile a contoallarovescia: visualizza la stringa s e chiama se stessa per n−1 altre volte. Il numero di righe risultanti sarà 1 + (n - 1), che corrisponde a n.

Per esempi semplici come questi, è forse più facile usare un ciclo for. Vedremo però più avanti degli esempi difficili da scrivere con un ciclo for ma facili con la ricorsione; meglio quindi cominciare subito a prendere mano.

5.9  Diagrammi di stack delle funzioni ricorsive

Nel Paragrafo 3.9, abbiamo usato un diagramma di stack per rappresentare lo stato di un programma durante una chiamata di funzione. Lo stesso tipo di diagramma può servire a capire come lavora una funzione ricorsiva.

Ogni volta che una funzione viene chiamata, Python crea un nuovo frame contenente le variabili locali definite all’interno della funzione ed i suoi parametri. Nel caso di una funzione ricorsiva, possono esserci contemporaneamente più frame riguardanti una stessa funzione.

La Figura 5.1 mostra il diagramma di stack della funzione contoallarovescia chiamata con n = 3.

---

Figure 5.1: Diagramma di stack.

---

Come al solito, il livello superiore dello stack è il frame di __main__. Questo frame è vuoto, perché in questo caso non vi abbiamo creato alcuna variabile né abbiamo passato alcun parametro.

I quattro frame di contoallarovescia hanno valori diversi del parametro n. Il livello inferiore dello stack, dove n=0, è chiamato caso base. Esso non effettua ulteriori chiamate ricorsive, quindi non ci sono ulteriori frame.

Come esercizio, disegnate il diagramma di stack della funzione stampa_n chiamata con s='Ciao' e n=2. Poi, scrivete una funzione di nome fai_n che accetti come argomenti un oggetto funzione e un numero n, e che chiami per n volte la funzione data.

5.10  Ricorsione infinita

Se una ricorsione non raggiunge mai un caso base, la chiamata alla funzione viene eseguita all’infinito ed in teoria il programma non giunge mai alla fine. Questa situazione è conosciuta come ricorsione infinita, e di solito non è considerata una buona cosa. Questo è un programma minimo che genera una ricorsione infinita:

def ricorsiva():
    ricorsiva()

Nella maggior parte degli ambienti, un programma con una ricorsione infinita non viene eseguito davvero all’infinito. Python stampa un messaggio di errore quando è stato raggiunto il massimo livello di ricorsione possibile:

  File "<stdin>", line 2, in ricorsiva
  File "<stdin>", line 2, in ricorsiva
  File "<stdin>", line 2, in ricorsiva
                  .   
                  .
                  .
  File "<stdin>", line 2, in ricorsiva
RuntimeError: Maximum recursion depth exceeded

Questo traceback è un po’ più lungo di quello che abbiamo visto nel capitolo precedente. Quando si verifica l’errore, nello stack ci sono oltre 1000 frame di chiamata di ricorsiva!

Se vi imbattete accidentalmente in una ricorsione infinita, rivedete la vostra funzione per accertare che esista un caso base che non genera una chiamata ricorsiva. E se c’è un caso base, controllate che venga sicuramente raggiunto.

5.11  Input da tastiera

I programmi che abbiamo scritto finora non accettano inserimenti di dati da parte dell’operatore, e si limitano a eseguire sempre le stesse operazioni.

Python comprende una funzione predefinita chiamata input che sospende il programma ed attende che l’operatore scriva qualcosa e confermi poi l’inserimento premendo il tasto Invio o Enter. A quel punto il programma riprende e input restituisce ciò che l’operatore ha inserito sotto forma di stringa. In Python 2, la funzione si chiama raw_input .

>>> testo = input()
Cosa stai aspettando?
>>> testo
'Cosa stai aspettando?'

Prima di chiamare la funzione, è buona norma stampare un messaggio che informa l’utente di ciò che deve inserire. Questo messaggio è chiamato prompt, e può essere passato come argomento a input :

>>> nome = input('Come...ti chiami?\n')
Come...ti chiami?
Artu', Re dei Bretoni!
>>> nome
'Artu', Re dei Bretoni!'

La sequenza \n alla fine del prompt rappresenta un ritorno a capo, un carattere speciale che provoca un’interruzione di riga. Ecco perché l’input dell’utente compare sulla riga successiva sotto al prompt.

Se il valore da inserire è un intero possiamo provare a convertire il valore inserito in int:

>>> prompt = "Qual è la velocità in volo di una rondine?\n"
>>> velocita = input(prompt)
Qual è la velocità in volo di una rondine?
42
>>> int(velocita)
42

Ma se la stringa inserita contiene qualcosa di diverso da dei numeri, si verifica un errore:

>>> velocita = input(prompt)
Qual è la velocità in volo di una rondine?
Cosa intendi, una rondine europea o africana?
>>> int(velocita)
ValueError: invalid literal for int() with base 10

Vedremo più avanti come trattare questo tipo di errori.

5.12  Debug

Quando si verifica un errore di sintassi o di runtime, il messaggio d’errore contiene molte informazioni, ma può essere sovrabbondante. Di solito le parti più utili sono:

• Che tipo di errore era, e
• Dove si è verificato.

Gli errori di sintassi di solito sono facili da trovare, con qualche eccezione. Gli spaziatori possono essere insidiosi, perché spazi e tabulazioni non sono visibili e siamo abituati a non tenerne conto.

>>> x = 5
>>>  y = 6
  File "<stdin>", line 1
    y = 6
    ^
IndentationError: unexpected indent

In questo esempio, il problema è che la seconda riga è erroneamente indentata di uno spazio, mentre dovrebbe stare al margine sinistro. Ma il messaggio di errore punta su y, portando fuori strada. In genere, i messaggi di errore indicano dove il problema è venuto a galla, ma il vero errore potrebbe essere in un punto precedente del codice, a volte anche nella riga precedente.

Lo stesso vale per gli errori di runtime.

Supponiamo di voler calcolare un rapporto segnale/rumore in decibel. La formula è SNR_db = 10 log₁₀ (P_segnale / P_rumore). In Python si può scrivere:

import math
potenza_segnale = 9
potenza_rumore = 10
rapporto = potenza_segnale // potenza_rumore
decibel = 10 * math.log10(rapporto)
print(decibel)

Se avviate questo programma, compare un messaggio di errore.

Traceback (most recent call last):
  File "snr.py", line 5, in ?
    decibel = 10 * math.log10(rapporto)
ValueError: math domain error

Il messaggio punta alla riga 5, ma lì non c’è niente di sbagliato. Per trovare il vero errore, può essere utile stampare il valore di rapporto, che risulta essere 0. Il problema sta nella riga 4, perché calcola una divisione intera anziché una normale divisione.

Prendetevi la briga di leggere attentamente i messaggi di errore, ma non date per scontato che tutto quello che dicono sia esatto.

5.13  Glossario

divisione intera:

Operatore, avente simbolo //, che divide due numeri e arrotonda il risultato all’intero inferiore (ovvero, verso l’infinito negativo).

operatore modulo:

Operatore matematico, denotato con il segno di percentuale (%), che restituisce il resto della divisione tra due operandi interi.

espressione booleana:

Espressione il cui valore è o vero (True) o falso (False).

operatore di confronto:

Un operatore che confronta due valori detti operandi: ==, !=, >, <, >=, e <=.

operatore logico:

Un operatore che combina due espressioni booleane: and, or, e not.

istruzione condizionale:

Istruzione che controlla il flusso di esecuzione del programma a seconda del verificarsi o meno di certe condizioni.

condizione:

Espressione booleana in un’istruzione condizionale che determina quale ramificazione debba essere seguita dal flusso di esecuzione.

istruzione composta:

Istruzione che consiste di un’intestazione terminante con i due punti (:) e di un corpo composto di una o più istruzioni indentate rispetto all’intestazione.

ramificazione:

Una delle sequenze di istruzioni alternative scritte in una istruzione condizionale.

condizioni in serie:

Istruzione condizionale con una serie di ramificazioni alternative.

condizione nidificata (o annidata):

Un’istruzione condizionale inserita in una ramificazione di un’altra istruzione condizionale.

istruzione di ritorno:

Un’istruzione che termina immediatamente una funzione e ritorna al chiamante.

ricorsione:

Procedura che chiama la stessa funzione attualmente in esecuzione.

caso base:

Ramificazione di un’istruzione condizionale, posta in una funzione ricorsiva, che non esegue a sua volta una chiamata ricorsiva.

ricorsione infinita:

Una ricorsione priva di un caso base, oppure che non lo raggiunge mai. Nell’evenienza, causa un errore in esecuzione.

5.14  Esercizi

>>> import time
>>> time.time()
1437746094.5735958

def ricorsione(n, s):
    if n == 0:
        print(s)
    else:
        ricorsione(n-1, n+s)

ricorsione(3, 0)

Gli esercizi seguenti utilizzano il modulo turtle, descritto nel Capitolo 4:

def disegna(t, lunghezza, n):
    if n == 0:
        return
    angolo = 50
    t.fd(lunghezza*n)
    t.lt(angolo)
    disegna(t, lunghezza, n-1)
    t.rt(2*angolo)
    disegna(t, lunghezza, n-1)
    t.lt(angolo)
    t.bk(lunghezza*n)

---

Figure 5.2: Una curva di Koch.

---

Buy this book at Amazon.com

Contribute

Pay what you want:

Small $1.00 USD Medium $5.00 USD Large $10.00 USD X-Large $20.00 USD XX-Large $50.00 USD

Are you using one of our books in a class?