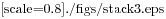Chapter 6 Funzioni produttive

Molte tra le funzioni di Python che abbiamo usato, come quelle matematiche, producono dei valori di ritorno. Ma quelle che abbiamo scritto noi finora sono tutte “vuote”: hanno un qualche effetto, come visualizzare un testo o muovere tartarughe, ma non hanno un valore di ritorno. In questo capitolo vedremo come si scrivono le funzioni che chiameremo “produttive”.

6.1 Valori di ritorno

La chiamata di una funzione genera un nuovo valore, che di solito viene associato ad una variabile o si usa come parte di un’espressione.

e = math.exp(1.0)
altezza = raggio * math.sin(radianti)

Le funzioni che abbiamo scritto finora sono “vuote”. Detto in modo semplicistico, non hanno valore di ritorno; ma a voler essere precisi, il loro valore di ritorno è None.

In questo capitolo scriveremo finalmente delle funzioni che restituiscono un valore e che chiameremo funzioni “produttive”. Facciamo un primo esempio con area, che calcola l’area di un cerchio di dato raggio:

def area(raggio):
    a = math.pi * raggio**2
    return a

Abbiamo già visto l’istruzione return, ma nel caso di una funzione produttiva questa istruzione include un’espressione. Il suo significato è: “ritorna immediatamente da questa funzione a quella chiamante e usa questa espressione come valore di ritorno”. L’espressione che rappresenta il valore di ritorno può essere anche complessa, e allora l’esempio precedente può essere riscritto in modo più compatto:

def area(raggio):
    return math.pi * raggio**2

D’altra parte, una variabile temporanea come a può rendere il programma più leggibile e semplificarne il debug.

Talvolta è necessario prevedere delle istruzioni di ritorno multiple, ciascuna all’interno di una ramificazione di un’istruzione condizionale:

def valore_assoluto(x):
    if x < 0:
        return -x
    else:
        return x

Dato che queste istruzioni return si trovano in rami diversi di una condizione alternativa, solo una di esse verrà effettivamente eseguita.

Non appena viene eseguita un’istruzione return, la funzione termina senza eseguire ulteriori istruzioni. Il codice che viene a trovarsi dopo l’istruzione return o in ogni altro punto che non può essere raggiunto dal flusso di esecuzione, è detto codice morto.

In una funzione produttiva è bene assicurarsi che ogni possibile flusso di esecuzione del programma porti ad un’uscita dalla funzione con un’istruzione return. Per esempio:

def valore_assoluto(x):
    if x < 0:
        return -x
    if x > 0:
        return x

Questa funzione ha un difetto, in quanto se x è uguale a 0, nessuna delle due condizioni è vera e la funzione termina senza incontrare un’istruzione return. Se il flusso di esecuzione arriva alla fine della funzione, il valore di ritorno sarà None, che non è di certo il valore assoluto di 0.

>>> print(valore_assoluto(0))
None

A proposito: Python contiene già la funzione abs che calcola il valore assoluto.

Per esercitarvi, scrivete una funzione di nome compara che prenda due valori, x e y, e restituisca 1 se x > y, 0 se x == y, e -1 se x < y.

6.2 Sviluppo incrementale

A mano a mano che scriverete funzioni di complessità maggiore, vi troverete a impiegare più tempo per il debug.

Per fare fronte a programmi via via più complessi, suggerisco una tecnica chiamata sviluppo incrementale. Lo scopo dello sviluppo incrementale è evitare lunghe sessioni di debug, aggiungendo e testando continuamente piccole parti di codice alla volta.

Come esempio, supponiamo che vogliate trovare la distanza tra due punti, note le coordinate (x₁, y₁) e (x₂, y₂). Per il teorema di Pitagora, la distanza è

distanza =

√

(x₂ − x₁)² + (y₂ − y₁)²

La prima cosa da considerare è l’aspetto che la funzione distanza deve avere in Python, chiarendo subito quali siano i parametri che deve avere la funzione e quale sia il valore di ritorno da ottenere.

Nel nostro caso i dati di partenza (o di input) sono i due punti, rappresentabili attraverso le loro coordinate (due coppie di numeri); il risultato (o output) è la distanza, espressa con un valore decimale.

Si può subito scrivere un primo abbozzo di funzione:

def distanza(x1, y1, x2, y2):
    return 0.0

Ovviamente questa prima versione non calcola ancora la distanza, ma restituisce sempre 0. Però è già una funzione sintatticamente corretta e può essere eseguita: potete quindi provarla prima di procedere a renderla più complessa.

Proviamo allora la nuova funzione, chiamandola con dei valori di esempio:

>>> distanza(1, 2, 4, 6)
0.0

Ho scelto questi valori in modo che la loro distanza orizzontale sia 3 e quella verticale 4. In tal modo, il risultato è pari a 5: l’ipotenusa di un triangolo rettangolo i cui cateti sono lunghi 3 e 4. Quando collaudiamo una funzione è sempre utile sapere prima il risultato.

A questo punto, abbiamo verificato che la funzione è sintatticamente corretta e possiamo cominciare ad aggiungere righe di codice nel corpo. Un passo successivo plausibile è quello di calcolare le differenze x₂ − x₁ e y₂ − y₁. Memorizzeremo queste differenze in due variabili temporanee che chiameremo dx e dy, e le mostreremo a video.

def distanza(x1, y1, x2, y2):
    dx = x2 - x1
    dy = y2 - y1
    print("dx è ", dx)
    print("dy è ", dy)
    return 0.0

Se la funzione è giusta, usando i valori di prima dovrebbe mostrare dx è 3 e dy è 4. Se i risultati coincidono, siamo sicuri che la funzione riceve correttamente i parametri ed elabora altrettanto correttamente i primi calcoli. Altrimenti, dovremo comunque controllare solo poche righe.

Proseguiamo con il calcolo della somma dei quadrati di dx e dy:

def distanza(x1, y1, x2, y2):
    dx = x2 - x1
    dy = y2 - y1
    dsquadr = dx**2 + dy**2
    print("dsquadr è: ", dsquadr)
    return 0.0

Di nuovo, eseguite il programma in questa fase e controllate il risultato, che nel nostro caso dovrebbe essere 25. Infine, usate la funzione radice quadrata math.sqrt per calcolare e restituire il risultato:

def distanza(x1, y1, x2, y2):
    dx = x2 - x1
    dy = y2 - y1
    dsquadr = dx**2 + dy**2
    risultato = math.sqrt(dsquadr)
    return risultato

Se tutto funziona, avete finito. Altrimenti, potete stampare per verifica il valore di risultato prima dell’istruzione return.

La versione definitiva della funzione non mostra nulla quando viene eseguita; restituisce solo un valore. Le istruzioni di stampa che avevamo inserito erano utili per il debug, ma una volta verificato che tutto funziona vanno rimosse. Pezzi di codice temporaneo come questi sono detti “impalcature”, perché sono di aiuto nella fase di costruzione del programma ma non fanno parte del prodotto finale.

Soprattutto agli inizi, non si dovrebbe mai aggiungere più di qualche riga di codice alla volta. Con l’esperienza, potrete scrivere e fare il debug di blocchi di codice sempre più corposi. In ogni caso, nelle prime fasi il processo di sviluppo incrementale potrà farvi risparmiare un bel po’ di tempo di debug.

Ecco i punti chiave di questa procedura:

Iniziate con un programma funzionante e fate piccoli cambiamenti: questo permetterà di scoprire facilmente dove sono localizzati gli eventuali errori.
Usate delle variabili per memorizzare i valori intermedi, così da poterli stampare e controllare.
Quando il programma funziona perfettamente, rimuovete le istruzioni temporanee e consolidate le istruzioni multiple in espressioni composte, sempre che questo non renda il programma troppo difficile da leggere.

Come esercizio, usate lo sviluppo incrementale per scrivere una funzione chiamata ipotenusa, che restituisca la lunghezza dell’ipotenusa di un triangolo rettangolo, dati i due cateti come parametri. Registrate ogni passo del processo di sviluppo man mano che procedete.

6.3 Composizione

Come potete ormai immaginare, è possibile chiamare una funzione dall’interno di un’altra funzione. Scriveremo come esempio una funzione che prende due punti geometrici, il centro di un cerchio ed un punto sulla sua circonferenza, e calcola l’area del cerchio.

Supponiamo che le coordinate del centro del cerchio siano memorizzate nelle variabili xc e yc, e quelle del punto sulla circonferenza in xp e yp. Innanzitutto, bisogna trovare il raggio del cerchio, che è pari alla distanza tra i due punti. La funzione distanza che abbiamo appena scritto, ci torna utile:

raggio = distanza(xc, yc, xp, yp)

Il secondo passo è trovare l’area del cerchio di quel raggio; anche questa funzione l’abbiamo già scritta:

risultato = area(raggio)

Incapsulando il tutto in una funzione otteniamo:

def area_cerchio(xc, yc, xp, yp):
    raggio = distanza(xc, yc, xp, yp)
    risultato = area(raggio)
    return risultato

Le variabili temporanee raggio e risultato sono utili per lo sviluppo e il debug ma, una volta constatato che il programma funziona, possiamo riscrivere la funzione in modo più conciso componendo le chiamate alle funzioni:

def area_cerchio(xc, yc, xp, yp):
    return area(distanza(xc, yc, xp, yp))

6.4 Funzioni booleane

Le funzioni possono anche restituire valori booleani (vero o falso), cosa che è spesso utile per includere al loro interno dei test, anche complessi. Per esempio:

def divisibile(x, y):
    if x % y == 0:
        return True
    else:
        return False

È prassi assegnare come nomi alle funzioni booleane dei predicati che, con accezione interrogativa, attendono una risposta sì/no; divisibile restituisce True o False per rispondere alla domanda se è vero o no che x è divisibile per y.

Facciamo un esempio:

>>> divisibile(6, 4)
False
>>> divisibile(6, 3)
True

Possiamo scrivere la funzione in modo ancora più conciso, visto che il risultato dell’operatore di confronto == è anch’esso un booleano, restituendolo direttamente:

def divisibile(x, y):
    return x % y == 0

Le funzioni booleane sono usate spesso nelle istruzioni condizionali:

if divisibile(x, y):
    print("x è divisibile per y")

Potreste pensare di scrivere in questo modo:

if divisibile(x, y) == True:
    print("x è divisibile per y")

ma il confronto supplementare è superfluo.

Scrivete ora, per esercizio, una funzione compreso_tra(x, y, z) che restituisca True se x ≤ y ≤ z o False altrimenti.

6.5 Altro sulla ricorsione

Abbiamo trattato solo una piccola parte di Python, ma è interessante sapere che questo sottoinsieme è già di per sé un linguaggio di programmazione completo: questo significa che con gli elementi che già conoscete potete esprimere qualsiasi tipo di elaborazione. Qualsiasi tipo di programma esistente potrebbe essere scritto usando solo le caratteristiche del linguaggio che avete appreso finora (aggiungendo solo alcuni comandi di controllo per gestire dispositivi come mouse, dischi, ecc.)

La prova di questa affermazione è un esercizio tutt’altro che banale affrontato per la prima volta da Alan Turing, uno dei pionieri dell’informatica (qualcuno potrebbe obiettare che in realtà era un matematico, ma molti dei primi informatici erano dei matematici). Di conseguenza la dimostrazione è chiamata Tesi di Turing. Per una trattazione più completa (ed accurata) della Tesi di Turing, consiglio il libro di Michael Sipser, Introduction to the Theory of Computation.

Per darvi un’idea di cosa potete fare con gli strumenti imparati finora, proveremo a valutare delle funzioni matematiche definite ricorsivamente. Una funzione ricorsiva è simile ad una definizione circolare, nel senso che la sua definizione contiene un riferimento alla cosa che si sta definendo. Una vera definizione circolare non è propriamente utile:

vorpale:: aggettivo usato per descrivere qualcosa di vorpale.

Sarebbe fastidioso trovare una definizione del genere in un vocabolario. D’altra parte, considerate la definizione della funzione matematica fattoriale (indicata da un numero seguito da un punto esclamativo, !), cioè:

		0! = 1
		n! = n (n−1)!

Questa definizione afferma che il fattoriale di 0 è 1 e che il fattoriale di ogni altro valore n, è n moltiplicato per il fattoriale di n−1.

Pertanto, 3! è 3 moltiplicato 2!, che a sua volta è 2 moltiplicato 1!, che a sua volta è 1 moltiplicato 0! che per definizione è 1. Riassumendo il tutto, 3! è uguale a 3 per 2 per 1 per 1, che fa 6.

Se potete scrivere una definizione ricorsiva di qualcosa, potete anche scrivere un programma Python per valutarla. Il primo passo è quello di decidere quali siano i parametri della funzione. Il fattoriale ha evidentemente un solo parametro, un intero:

def fattoriale(n):

Se l’argomento è 0, dobbiamo solo restituire il valore 1:

def fattoriale(n):
    if n == 0:
        return 1

Altrimenti, e questa è la parte interessante, dobbiamo fare una chiamata ricorsiva per trovare il fattoriale di n−1 e poi moltiplicare questo valore per n:

def fattoriale(n):
    if n == 0:
        return 1
    else:
        ricors = fattoriale(n-1)
        risultato = n * ricors
        return risultato

Il flusso di esecuzione del programma è simile a quello di contoallarovescia del Paragrafo 5.8. Se chiamiamo fattoriale con il valore 3:

Dato che 3 è diverso da 0, seguiamo il ramo else e calcoliamo il fattoriale di n-1...

Dato che 2 è diverso da 0, seguiamo il ramo else e calcoliamo il fattoriale di n-1...
Dato che 1 è diverso da 0, seguiamo il ramo else e calcoliamo il fattoriale di n-1...
Dato che 0 è uguale a 0, seguiamo il primo ramo e ritorniamo 1 senza fare altre chiamate ricorsive.
Il valore di ritorno (1) è moltiplicato per n, che è 1, e il risultato ritorna al chiamante.
Il valore di ritorno (1) è moltiplicato per n, che è 2, e il risultato ritorna al chiamante.

Il valore di ritorno (2) è moltiplicato per n, che è 3, e il risultato, 6, diventa il valore di ritorno della funzione che ha fatto partire l’intera procedura.

La Figura 6.1 mostra il diagramma di stack per l’intera sequenza di chiamate di funzione:

Figure 6.1: Diagramma di stack .

I valori di ritorno sono illustrati mentre vengono passati all’indietro verso l’alto della pila. In ciascun frame, il valore di ritorno è quello di risultato, che è il prodotto di n e ricors.

Notate che nell’ultimo frame le variabili locali ricors e risultato non esistono, perché il ramo che le crea non viene eseguito.

6.6 Salto sulla fiducia

Seguire il flusso di esecuzione è il modo giusto di leggere i programmi, ma può diventare rapidamente labirintico se le dimensioni del codice aumentano. Un metodo alternativo è quello che io chiamo “salto sulla fiducia”. Quando arrivate ad una chiamata di funzione, invece di seguire il flusso di esecuzione, date per scontato che la funzione chiamata si comporti correttamente e che restituisca il valore esatto.

Nei fatti, già praticate questo atto di fede quando utilizzate le funzioni predefinite: se chiamate math.cos o math.exp, non andate a controllare l’implementazione delle funzioni, ma date per scontato che funzionino a dovere perché le hanno scritte dei validi programmatori.

Lo stesso si può dire per le funzioni che scrivete voi: quando, nel Paragrafo 6.4, abbiamo scritto la funzione divisibile che controlla se un numero è divisibile per un altro, e abbiamo verificato che la funzione è corretta,—controllando e provando il codice—possiamo poi usarla senza doverla ricontrollare di nuovo.

Idem quando abbiamo chiamate ricorsive: invece di seguire il flusso di esecuzione, potete partire dal presupposto che la chiamata ricorsiva funzioni (restituendo il risultato corretto), per poi chiedervi: “Supponendo che io trovi il fattoriale di n−1, posso calcolare il fattoriale di n?”. È chiaro che potete farlo, moltiplicando per n.

Certo, è strano partire dal presupposto che una funzione sia giusta quando non avete ancora finito di scriverla, ma non per nulla si chiama "salto sulla fiducia"!

6.7 Un altro esempio

Dopo il fattoriale, l’esempio più noto di funzione matematica definita ricorsivamente è la funzione fibonacci, che ha la seguente definizione: (vedere http://it.wikipedia.org/wiki/Successione_di_Fibonacci):

		fibonacci(0) = 0
		fibonacci(1) = 1
		fibonacci(n) = fibonacci(n−1) + fibonacci(n−2)

Che tradotta in Python è:

def fibonacci(n):
    if n == 0:
        return 0
    elif  n == 1:
        return 1
    else:
        return fibonacci(n-1) + fibonacci(n-2)

Con una funzione simile, provare a seguire il flusso di esecuzione vi farebbe scoppiare la testa anche con valori di n piuttosto piccoli. Ma in virtù del “salto sulla fiducia”, dando per scontato che le due chiamate ricorsive funzionino correttamente, è chiaro che la somma dei loro valori di ritorno sarà corretta.

6.8 Controllo dei tipi

Cosa succede se chiamiamo fattoriale passando 1.5 come argomento?

>>> fattoriale(1.5)
RuntimeError: Maximum recursion depth exceeded

Parrebbe una ricorsione infinita. Come mai? La funzione ha un caso base—quando n == 0. Ma se n non è intero, manchiamo il caso base e la ricorsione non si ferma più.

Alla prima chiamata ricorsiva, infatti, il valore di n è 0.5. Alla successiva diventa -0.5. Da lì in poi, il valore passato alla funzione diventa ogni volta più piccolo di una unità (cioè più negativo) e non potrà mai essere 0.

Abbiamo due scelte: possiamo tentare di generalizzare la funzione fattoriale per farla funzionare anche nel caso di numeri a virgola mobile, o possiamo far controllare alla funzione se il parametro passato è del tipo corretto. La prima possibilità è chiamata in matematica funzione gamma, ma è un po’ oltre gli scopi di questo libro; quindi sceglieremo la seconda alternativa.

Possiamo usare la funzione predefinita isinstance per verificare il tipo di argomento. E già che ci siamo, ci accerteremo anche che il numero sia positivo:

def fattoriale(n):
    if not isinstance(n, int):
        print("Il fattoriale è definito solo per numeri interi.")
        return None
    elif n < 0:
        print("Il fattoriale non è definito per interi negativi.")
        return None
    elif n == 0:
        return 1
    else:
        return n * fattoriale(n-1)

Il primo caso base gestisce i numeri non interi; il secondo, gli interi negativi. In entrambi i casi, il programma mostra un messaggio di errore e restituisce il valore None per indicare che qualcosa non ha funzionato:

>>> print(fattoriale('alfredo'))
Il fattoriale è definito solo per numeri interi.
None
>>> print(fattoriale(-2))
Il fattoriale non è definito per interi negativi.
None

Se superiamo entrambi i controlli, possiamo essere certi che n è un intero positivo oppure zero, e che la ricorsione avrà termine.

Questo programma mostra lo schema di funzionamento di una condizione di guardia. I primi due controlli agiscono da “guardiani”, difendendo il codice che segue da valori che potrebbero causare errori. Le condizioni di guardia rendono possibile provare la correttezza del codice.

Nel Paragrafo 11.4 vedremo un’alternativa più flessibile alla stampa di messaggi di errore: sollevare un’eccezione.

6.9 Debug

La suddivisione di un programma di grandi dimensioni in funzioni più piccole, crea dei naturali punti di controllo per il debug. Se una funzione non va, ci sono tre possibilità da prendere in esame:

C’è qualcosa di sbagliato negli argomenti che la funzione sta accettando: è violata una precondizione.
C’è qualcosa di sbagliato nella funzione: è violata una postcondizione.
C’è qualcosa di sbagliato nel valore di ritorno o nel modo in cui viene usato.

Per escludere la prima possibilità, potete aggiungere un’istruzione di stampa all’inizio della funzione per visualizzare i valori dei parametri (e magari i loro tipi). O potete scrivere del codice che controlla esplicitamente le precondizioni.

Se i parametri sembrano corretti, aggiungete un’istruzione di stampa prima di ogni istruzione return e visualizzate il valore di ritorno. Se possibile, controllate i risultati calcolandoveli a parte. Cercate di chiamare la funzione fornendole dei valori che permettono un agevole controllo del risultato (come nel Paragrafo 6.2).

Se la funzione sembra a posto, controllate la chiamata per essere sicuri che il valore di ritorno venga usato correttamente (e soprattutto, venga usato!).

Aggiungere istruzioni di stampa all’inizio e alla fine di una funzione può aiutare a rendere più chiaro il flusso di esecuzione. Ecco una versione di fattoriale con delle istruzioni di stampa:

def fattoriale(n):
    spazi = ' ' * (4 * n)
    print(spazi, 'fattoriale', n)
    if n == 0:
        print(spazi, 'ritorno 1')
        return 1
    else:
        ricors = fattoriale(n-1)
        risultato = n * ricors
        print(spazi, 'ritorno ', risultato)
        return risultato

spazi è una stringa di caratteri di spaziatura che controlla l’indentazione dell’output. Ecco il risultato di fattoriale(4) :

                 fattoriale 4
             fattoriale 3
         fattoriale 2
     fattoriale 1
 fattoriale 0
 ritorno 1
     ritorno 1
         ritorno 2
             ritorno 6
                 ritorno 24

Se il flusso di esecuzione vi confonde, questo tipo di output può aiutarvi. Ci vuole un po’ di tempo per sviluppare delle “impalcature” efficaci, ma in compenso queste possono far risparmiare molto tempo di debug.

6.10 Glossario

variabile temporanea:: Variabile usata per memorizzare un risultato intermedio durante un calcolo complesso.
codice morto:: Parte di un programma che non può mai essere eseguita, spesso perché compare dopo un’istruzione return.
sviluppo incrementale:: Tecnica di sviluppo del programma inteso ad evitare lunghe sessioni di debug, aggiungendo e provando piccole porzioni di codice alla volta.
impalcatura:: Codice temporaneo inserito solo nella fase di sviluppo del programma e che non fa parte della versione finale.
condizione di guardia:: Schema di programmazione che usa una condizione per controllare e gestire le circostanze che possono causare un errore.

6.11 Esercizi

Esercizio 1

Disegnate un diagramma di stack del seguente programma. Che cosa visualizza?

def b(z):
    prod = a(z, z)
    print(z, prod)
    return prod

def a(x, y):
    x = x + 1
    return x * y

def c(x, y, z):
    totale = x + y + z
    quadrato = b(totale)**2
    return quadrato

x = 1
y = x + 1
print(c(x, y+3, x+y))

Esercizio 2

La funzione di Ackermann, A(m, n), è così definita:

A(m, n) =

⎧
⎪
⎨
⎪
⎩

n+1	se m = 0
A(m−1, 1)	se m > 0 e n = 0
A(m−1, A(m, n−1))	se m > 0 e n > 0.

Vedere anche http://it.wikipedia.org/wiki/Funzione_di_Ackermann. Scrivete una funzione di nome ack che valuti la funzione di Ackermann. Usate la vostra funzione per calcolare ack(3, 4), vi dovrebbe risultare 125. Cosa succede per valori maggiori di m e n? Soluzione: http://thinkpython2.com/code/ackermann.py.

Esercizio 3

Un palindromo è una parola che si legge nello stesso modo sia da sinistra verso destra che viceversa, come “ottetto” e “radar”. In termini ricorsivi, una parola è un palindromo se la prima e l’ultima lettera sono uguali e ciò che resta in mezzo è un palindromo.

Quelle che seguono sono funzioni che hanno una stringa come parametro e restituiscono rispettivamente la prima lettera, l’ultima lettera, e quelle in mezzo:

def prima(parola):
    return parola[0]

def ultima(parola):
    return parola[-1]

def mezzo(parola):
    return parola[1:-1]

Vedremo meglio come funzionano nel Capitolo 8.

Scrivete queste funzioni in un file script palindromo.py e provatele. Cosa succede se chiamate mezzo con una stringa di due lettere? E di una lettera? E con la stringa vuota, che si scrive '' e non contiene caratteri?
Scrivete una funzione di nome palindromo che riceva una stringa come argomento e restituisca True se è un palindromo e False altrimenti. Ricordate che potete usare la funzione predefinita len per controllare la lunghezza di una stringa.

Soluzione: http://thinkpython2.com/code/palindrome_soln.py.

Esercizio 4

Un numero, a, è una potenza di b se è divisibile per b e a/b è a sua volta una potenza di b. Scrivete una funzione di nome potenza che prenda come parametri a e b e che restituisca True se a è una potenza di b. Nota: dovete pensare bene al caso base.

Esercizio 5

Il massimo comun divisore (MCD) di due interi a e b è il numero intero più grande che divide entrambi senza dare resto.

Un modo per trovare il MCD di due numeri si basa sull’osservazione che, se r è il resto della divisione tra a e b, allora mcd(a, b) = mcd(b, r). Come caso base, possiamo usare mcd(a, 0) = a.

Scrivete una funzione di nome mcd che abbia come parametri a e b e restituisca il loro massimo comun divisore.

Fonte: Questo esercizio è basato su un esempio in Structure and Interpretation of Computer Programs di Abelson e Sussman.

Buy this book at Amazon.com

Contribute

If you would like to make a contribution to support my books, you can use the button below. Thank you!

Are you using one of our books in a class?

We'd like to know about it. Please consider filling out this short survey.